Question
Question: The variation of radial probability density \({R^2}\left( r \right)\) as a function of distance r of...
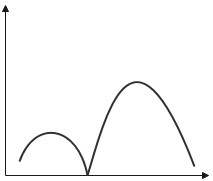
The variation of radial probability density R2(r) as a function of distance r of the electron from the nucleus for 3p- orbital.
Solution
To answer this question, you must recall radial probability curves for various orbitals. Radial probability density curve helps us in finding the points in space with respect to the nucleus where the probability of finding electrons is maximum and also tells the points where the probability is zero. The points where the probability density of electrons is zero are known as nodes.
Formula used:
Number of radial nodes =n−l−1
Where, n is the principal quantum number
And l is the azimuthal quantum number
Complete step by step answer:
Probability density of finding an electron at a point can be defined as the probability per unit volume, with the limit that the volume is infinitesimally. Knowing this, we can define the radial probability distribution at a certain radius as the probability density of electrons in an infinitesimally thin spherical shell. Thus, we can say that radial probability distribution is a function of radial distance from the nucleus. The points where radial probability distribution is zero are called radial nodes.
We know that radial nodes in a given orbital are given by the formula,
Number of radial nodes=n−l−1.
We need to find the radial nodes for the 3porbital, which has the principal quantum number n=3 and the azimuthal quantum number, l=1
Using the formula, we get the number of radial nodes=3−1−1=1.
Thus, the variation of the radial probability density for 3p orbital can be given as,
Note:
Apart from radial nodes, there is another type of node that exists in an atom. This is known as angular node. While radial nodes are spherical and at a fixed radius, the angular nodes are flat and at a fixed angle.
