Question
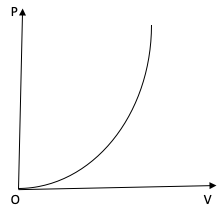
Question: The variation of pressure P with volume V for an ideal diatomic gas is parabolic as shown in the fig...
The variation of pressure P with volume V for an ideal diatomic gas is parabolic as shown in the figure. The molar specific heat of the gas during this process is?
A.59R
B.617R
C.53R
D.58R
Solution
From the PV curve given in the question, we will find the relation between P and V, and then by comparing it with the relation for the polytropic process (PVx=const.) we can find the value of ‘x’. Then by using the below given formula, molar specific heat of the polytropic process can be found.
C=2fR+1−xR
Complete step by step answer:
The PV curve of the diatomic gas is a parabola. Therefore, we can write
PαV2
⇒PV−2= constant
For a polytropic process, the relation between P and V is PVx= constant. On comparing the two equations we get, x=−2.
Now, in case of a diatomic gas, the degree of freedom is 5, that is, f=5.
The molar specific heat of a gas undergoing polytropic process is given by,
C=2fR+1−xR
Substituting the values of ‘f’ and ‘x’, we get,
C=25R+1−(−2)R
⇒C=25R+1+2R
⇒C=25R+3R
⇒C=615R+2R
⇒C=617R
Thus, the molar specific heat of the given diatomic gas is 617R.
Hence option B is correct.
Note:
The molar specific heat of gases is the amount of heat energy required by 1 mole of the gas to raise its temperature by 1 degree Celsius. There are two types of molar specific heats of gases. When measured at constant pressure, it is called the molar specific heat at constant pressure, denoted by Cp. When it is measured at constant volume, then it is called molar specific heat at constant volume, denoted by Cv. Both these quantities are related as Cp=Cv+R.
