Question

The variance of the numbers 8, 21, 34, 47, ..., 320 is ____.

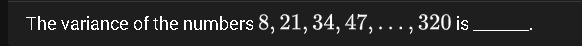
Answer 1

8788

Answer 2

We are given an arithmetic progression (AP) with first term

$$a = 8,$$

common difference

$$d = 13,$$

and last term

$$l = 320.$$

1. Number of terms (n):

$$l = a + (n-1)d \implies 320 = 8 + (n-1) \times 13.$$ $$\implies (n-1) \times 13 = 312 \implies n-1 = 24 \implies n = 25.$$

2. Variance of an AP:

For an AP, the variance is given by

$$\sigma^2 = \frac{d^2 (n^2 - 1)}{12}.$$

Substituting $d = 13$ and $n = 25$,

$$\sigma^2 = \frac{13^2 (25^2 - 1)}{12} = \frac{169 \times (625 - 1)}{12} = \frac{169 \times 624}{12}.$$

Simplifying,

$$\frac{624}{12} = 52 \quad \implies \quad \sigma^2 = 169 \times 52 = 8788.$$