Question

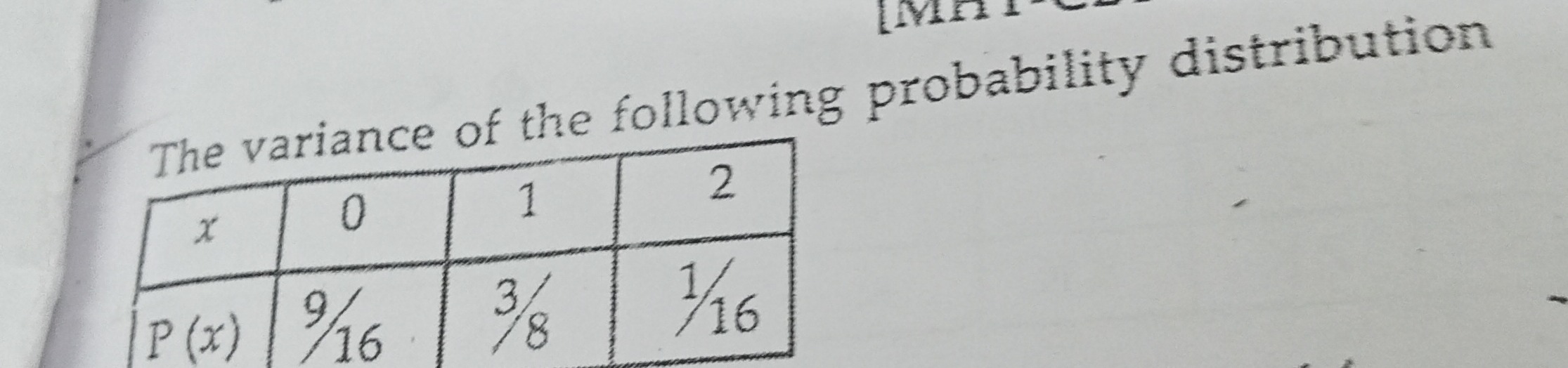
The variance of the following probability distribution

x	0	1	2
P(x)	9/16	3/8	1/16

Answer 1

3/8

Answer 2

To find the variance of the probability distribution:

1. Calculate the expected value (mean):

   $$E(x) = 0\cdot\frac{9}{16} + 1\cdot\frac{3}{8} + 2\cdot\frac{1}{16} = \frac{0}{16} + \frac{6}{16} + \frac{2}{16} = \frac{8}{16} = \frac{1}{2}$$

2. Calculate the expected value of $x^2$:

   $$E(x^2) = 0^2\cdot\frac{9}{16} + 1^2\cdot\frac{3}{8} + 2^2\cdot\frac{1}{16} = 0 + \frac{6}{16} + \frac{4}{16} = \frac{10}{16} = \frac{5}{8}$$

3. Determine the variance:

   $$\text{Variance} = E(x^2) - [E(x)]^2 = \frac{5}{8} - \left(\frac{1}{2}\right)^2 = \frac{5}{8} - \frac{1}{4} = \frac{5}{8} - \frac{2}{8} = \frac{3}{8}$$

Therefore, the variance of the probability distribution is $\frac{3}{8}$.