Question

The variable line drawn through the point $\left( 1,3 \right)$ meets the $x-axis$ at $A$ and $y-axis$ at $B$. If the rectangle $OAPB$ is completed. Where $O$ is the origin, then locus of $P$ is?
A. $\dfrac{1}{y}+\dfrac{3}{x}=1$.
B. $x+3y=1$
C. $\dfrac{1}{x}+\dfrac{3}{y}=1$
D. $3x+y=1$

Answer 1

In this problem we need to find the locus of the point $P$ according to the given conditions. Given that the line passes through the point $\left( 1,3 \right)$ which is assumed to be $C$ meets the $x-axis$ at $A$ and $y-axis$ at $B$. So, we will assume the coordinates of the points $A$ and $B$ as $\left( h,0 \right)$, $\left( 0,k \right)$ respectively. Now we will calculate the slope of the line $BC$, $AC$. Use the geometry rule which is the slope of the lines $BC$, $AC$ are equal because they both are single lines. Now simplify the equation and replace $h$, $k$ with $x$, $y$ respectively to get the required result.

Complete step-by-step answer:
Given data, The variable line drawn through the point $\left( 1,3 \right)$ meets the $x-axis$ at $A$ and $y-axis$ at $B$ and the rectangle $OAPB$ is completed. Where $O$ is the origin. The diagrammatic representation of the above data is given by

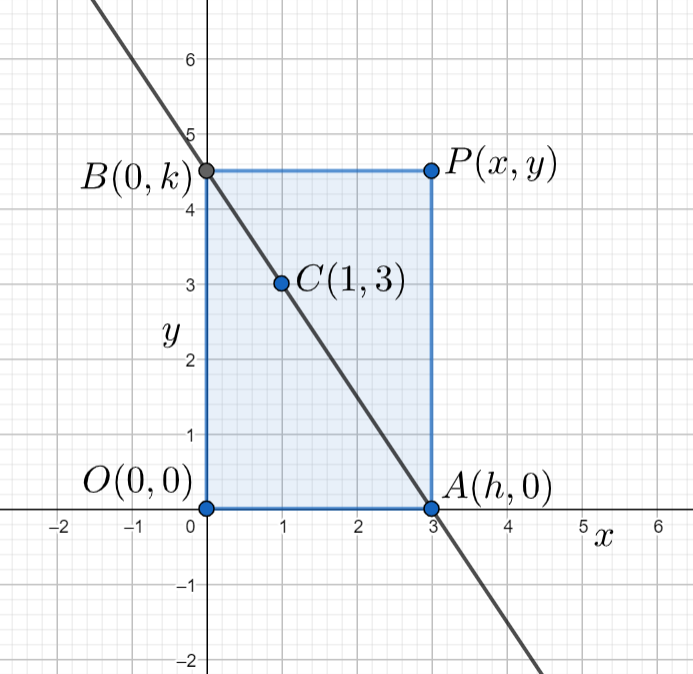
Let the coordinates of the points $A$ and $B$ are assumed to be $\left( h,0 \right)$, $\left( 0,k \right)$ respectively.
Now the slope of the line $BC$ will be given by
$m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$
Substituting the values $\left( {{x}_{1}},{{y}_{1}} \right)=\left( 0,k \right)$, $\left( {{x}_{2}},{{y}_{2}} \right)=\left( 1,3 \right)$ in the above equation, then we will get
$\begin{aligned} & m=\dfrac{3-k}{1-0} \\\ & \Rightarrow m=\dfrac{3-k}{1} \\\ \end{aligned}$
Now the slope of the line $AC$ will be calculated by substituting $\left( {{x}_{1}},{{y}_{1}} \right)=\left( h,0 \right)$, $\left( {{x}_{2}},{{y}_{2}} \right)=\left( 1,3 \right)$ in $m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$, then we will get
$\begin{aligned} & m=\dfrac{3-0}{1-h} \\\ & \Rightarrow m=\dfrac{3}{1-h} \\\ \end{aligned}$
Now the line $BC$, $AC$ represents the same line, so the slopes of the two lines should be equal, then we will have
$\dfrac{3-k}{1}=\dfrac{3}{1-h}$
Doing cross multiplication in the above equation, then we will get
$\left( 3-k \right)\left( 1-h \right)=3$
Using distribution law of multiplication in the above equation, then we will have
$3-3h-k+hk=3$
Cancelling the term $3$ which is on both sides of the above equation and divide whole equation with $hk$, then we will get
$\dfrac{-3h-k+hk}{hk}=0$
Simplifying the above equation by using mathematical operations, then we will have
$\begin{aligned} & \dfrac{-3h}{hk}-\dfrac{k}{hk}+\dfrac{hk}{hk}=0 \\\ & \Rightarrow -\dfrac{3}{k}-\dfrac{1}{h}+1=0 \\\ & \Rightarrow \dfrac{1}{h}+\dfrac{3}{k}=1 \\\ \end{aligned}$
Replace the terms $h$, $k$ with $x$, $y$ respectively in the above equation, then we will get
$\dfrac{1}{x}+\dfrac{3}{y}=1$

So, the correct answer is “Option c”.

Note: We can also use the collinear property form the points $A$, $C$, $B$ and simplify the determinant obtained to get the required result. Here we need to solve the determinant $\left| \begin{matrix} h & 0 & 1 \\\ 1 & 3 & 1 \\\ 0 & k & 1 \\\ \end{matrix} \right|=0$ which shows that the points are collinear.