Question

The vapour pressures of A and B at 25°C are 90 mm Hg and 15 mm Hg respectively. If A and B are mixed such that the mole fraction of A in the mixture is 0.6, then the mole fraction of B in the vapour phase is $x \times 10^{-1}$. The value of x is ___. (Nearest integer)

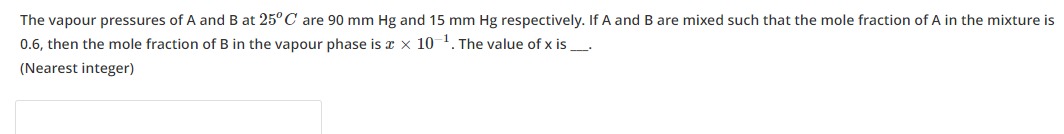
Answer 1

1

Answer 2

The vapor pressures of pure A and B are given as $P_A^0 = 90$ mm Hg and $P_B^0 = 15$ mm Hg.

The mole fraction of A in the liquid mixture is $x_A = 0.6$.

The mole fraction of B in the liquid mixture is $x_B = 1 - x_A = 1 - 0.6 = 0.4$.

According to Raoult's Law, the partial pressure of a component in the vapor phase above the solution is given by:

$P_A = x_A \times P_A^0$

$P_B = x_B \times P_B^0$

Substitute the given values:

$P_A = 0.6 \times 90 \text{ mm Hg} = 54 \text{ mm Hg}$

$P_B = 0.4 \times 15 \text{ mm Hg} = 6 \text{ mm Hg}$

According to Dalton's Law of partial pressures, the total pressure of the solution is the sum of the partial pressures:

$P_{total} = P_A + P_B$

$P_{total} = 54 \text{ mm Hg} + 6 \text{ mm Hg} = 60 \text{ mm Hg}$

The mole fraction of a component in the vapor phase is given by the ratio of its partial pressure to the total pressure:

$y_B = \frac{P_B}{P_{total}}$

$y_B = \frac{6 \text{ mm Hg}}{60 \text{ mm Hg}} = \frac{1}{10} = 0.1$

The problem states that the mole fraction of B in the vapor phase is $x \times 10^{-1}$.

So, $y_B = x \times 10^{-1}$.

We have calculated $y_B = 0.1$.

$0.1 = x \times 10^{-1}$

$0.1 = x \times 0.1$

$x = \frac{0.1}{0.1} = 1$

The value of x is 1. The nearest integer value of x is 1.