Solveeit Logo
Login

Question

Question: The values of \(x\) satisfying \(\tan ({\sec ^{ - 1}}x) = \sin \left( {{{\cos }^{ - 1}}\dfrac{1}{{\s...

The values of xx satisfying tan⁡(sec⁡−1x)=sin⁡(cos⁡−115)\tan ({\sec ^{ - 1}}x) = \sin \left( {{{\cos }^{ - 1}}\dfrac{1}{{\sqrt 5 }}} \right) is
A) ±53 \pm \dfrac{{\sqrt 5 }}{3}
B) ±35 \pm \dfrac{3}{{\sqrt 5 }}
C) ±35 \pm \dfrac{{\sqrt 3 }}{5}
D) ±35 \pm \dfrac{3}{5}

Explanation

Solution

n the above question we can see that we have trigonometric ratios. We will first draw a right angle triangle and then we simplify the equation according to that, Then we will try to simplify the trigonometric ratio in their simple form as
sec⁡θ=1cos⁡θ\sec \theta = \dfrac{1}{{\cos \theta }}
We will assume that
sec⁡−1x=θ{\sec ^{ - 1}}x = \theta
We can write this as
1sec⁡x=θ\dfrac{1}{{\sec }}x = \theta
By cross multiplication it gives us
sec⁡θ=x\sec \theta = x .

Complete step by step answer:
Here we have tan⁡(sec⁡−1x)=sin⁡(cos⁡−115)\tan ({\sec ^{ - 1}}x) = \sin \left( {{{\cos }^{ - 1}}\dfrac{1}{{\sqrt 5 }}} \right)
Let us first draw the right angle triangle:

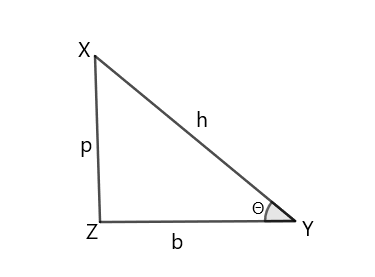
In the above figure we have XYZ is a right angled triangle and
∠XYZ=θ\angle XYZ = \theta
Here p is the perpendicular, b stands for base and h is the hypotenuse of the triangle.
Let us first take the left hand side of the equation:
Now let us assume that sec⁡−1x=θ{\sec ^{ - 1}}x = \theta .
We can write it as sec⁡θ=x\sec \theta = x .
We know that
sec⁡θ=1cos⁡θ\sec \theta = \dfrac{1}{{\cos \theta }} , so by putting this we can write
1cos⁡θ=x⇒cos⁡θ=1x\dfrac{1}{{\cos \theta }} = x \Rightarrow \cos \theta = \dfrac{1}{x}
We know that the trigonometric ratio of the cosine function :
cos⁡θ=bh\cos \theta = \dfrac{b}{h}
By comparing here we have
b=1,h=xb = 1,h = x
Now by Pythagoras theorem we can calculate the perpendicular i.e.
p=h2−b2p = \sqrt {{h^2} - {b^2}}
By putting the value it gives us
p=x2−1p = \sqrt {{x^2} - 1}
We can write them now in tangent form i.e.
tan⁡=pb\tan = \dfrac{p}{b}
By substituting the values of base and perpendicular we have:
tan⁡θ=x2−11\tan \theta = \dfrac{{\sqrt {{x^2} - 1} }}{1}
From the above we can calculate the value of θ\theta by transferring tan to the other side i.e.
θ=x2−11×1tan⁡\theta = \dfrac{{\sqrt {{x^2} - 1} }}{1} \times \dfrac{1}{{\tan }}
The above expression can also be written as
θ=tan⁡−1(x2−1)\theta = {\tan ^{ - 1}}\left( {\sqrt {{x^2} - 1} } \right)
From the above we have assumed that
sec⁡−1x=θ{\sec ^{ - 1}}x = \theta .
Now we can put this value back in the original form of the equation i.e.
tan⁡(tan⁡−1x2−1)\tan \left( {{{\tan }^{ - 1}}\sqrt {{x^2} - 1} } \right)
We will now solve the right hand side of the equation i.e.
sin⁡(cos⁡−115)\sin \left( {{{\cos }^{ - 1}}\dfrac{1}{{\sqrt 5 }}} \right)
Let us assume that
(cos⁡−115)=θ\left( {{{\cos }^{ - 1}}\dfrac{1}{{\sqrt 5 }}} \right) = \theta
On simplifying it gives us
cos⁡θ=15\cos \theta = \dfrac{1}{{\sqrt 5 }}
Now we know that
cos⁡θ=bh\cos \theta = \dfrac{b}{h}
By comparing here we have
b=1,h=5b = 1,h = \sqrt 5
Now by Pythagoras theorem we can calculate the perpendicular i.e.
p=h2−b2p = \sqrt {{h^2} - {b^2}}
By putting the value it gives us
p=(5)2−12p = \sqrt {{{(\sqrt 5 )}^2} - {1^2}}
On simplifying
5−1=4\sqrt {5 - 1} = \sqrt 4
It gives us the value
p=2p = 2
We can write them now in sine form i.e.
sin⁡=ph\sin = \dfrac{p}{h}
By substituting the values of hypotenuse and perpendicular we have:
sin⁡θ=25\sin \theta = \dfrac{2}{{\sqrt 5 }}
We can calculate the value of θ\theta by transferring sin to the other side i.e.
θ=25×1sin⁡\theta = \dfrac{2}{{\sqrt 5 }} \times \dfrac{1}{{\sin }} And,
1sin⁡\dfrac{1}{{\sin }} can be written as
sin⁡−1{\sin ^{ - 1}}
So it gives us
θ=sin⁡−125\theta = {\sin ^{ - 1}}\dfrac{2}{{\sqrt 5 }}
Again we have assume here that
(cos⁡−115)=θ\left( {{{\cos }^{ - 1}}\dfrac{1}{{\sqrt 5 }}} \right) = \theta
Now by putting the value of θ\theta back in the equation we have
sin⁡(sin⁡−125)\sin \left( {{{\sin }^{ - 1}}\dfrac{2}{{\sqrt 5 }}} \right)
So the new equation here we have
tan⁡(tan⁡−1x2−1)=sin⁡(sin⁡−125)\tan \left( {{{\tan }^{ - 1}}\sqrt {{x^2} - 1} } \right) = \sin \left( {{{\sin }^{ - 1}}\dfrac{2}{{\sqrt 5 }}} \right)
We will apply the basic trigonometric identities such as sin⁡(sin⁡−1x)=x\sin ({\sin ^{ - 1}}x) = x and tan⁡(tan⁡−1x)=x\tan ({\tan ^{ - 1}}x) = x
By applying these identities in the above we can write them as:
x2−1=25\sqrt {{x^2} - 1} = \dfrac{2}{{\sqrt 5 }}
We will square both the sides of the equation:

(x2−1)2=(25)2{\left( {\sqrt {{x^2} - 1} } \right)^2} = {\left( {\dfrac{2}{{\sqrt 5 }}} \right)^2}
By squaring both the sides of the equation we have :
x2−1=45{x^2} - 1 = \dfrac{4}{5}
We will cross multiply them and solve them:
5(x2−1)=4⇒5x2−5=45\left( {{x^2} - 1} \right) = 4 \Rightarrow 5{x^2} - 5 = 4
By grouping the similar term together:
5x2=5+4⇒5x2=95{x^2} = 5 + 4 \Rightarrow 5{x^2} = 9
It gives us
x2=95{x^2} = \dfrac{9}{5}
We have to find the value of xx , so we have :
x=95⇒x=±35x = \sqrt {\dfrac{9}{5}} \Rightarrow x = \pm \dfrac{3}{{\sqrt 5 }}
Hence the correct option is option (B) ±35 \pm \dfrac{3}{{\sqrt 5 }}.

Note:
We should note that in the above solution we have assumed
(cos⁡−115)=θ\left( {{{\cos }^{ - 1}}\dfrac{1}{{\sqrt 5 }}} \right) = \theta
We can write
cos⁡−1=1cos⁡{\cos ^{ - 1}} = \dfrac{1}{{\cos }}
So by putting this in the above expression we can write
1cos⁡×15=θ\dfrac{1}{{\cos }} \times \dfrac{1}{{\sqrt 5 }} = \theta
By cross multiplication of cosine or by transferring cosine to the other side, we have:
cos⁡θ=15\cos \theta = \dfrac{1}{{\sqrt 5 }}