Solveeit Logo
Login

Question

Question: The value(s) of $\int_{0}^{1} \frac{x^4(1-x)^4}{1+x^2}dx$ is (are)...

The value(s) of ∫01x4(1−x)41+x2dx\int_{0}^{1} \frac{x^4(1-x)^4}{1+x^2}dx is (are)

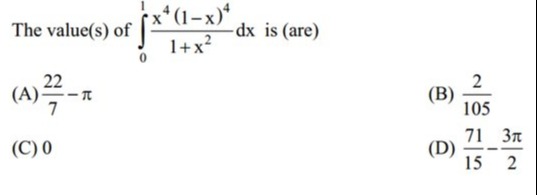
A

227−π\frac{22}{7} - \pi

B

2105\frac{2}{105}

C

0

D

7115−3π2\frac{71}{15} - \frac{3\pi}{2}

Answer

227−π\frac{22}{7} - \pi

Explanation

Solution

To evaluate the integral I=∫01x4(1−x)41+x2dxI = \int_{0}^{1} \frac{x^4(1-x)^4}{1+x^2}dx, we first expand the numerator:

x4(1−x)4=(x(1−x))4=(x−x2)4=x8−4x7+6x6−4x5+x4x^4(1-x)^4 = (x(1-x))^4 = (x-x^2)^4 = x^8 - 4x^7 + 6x^6 - 4x^5 + x^4.

Now, we perform polynomial long division of x8−4x7+6x6−4x5+x4x^8 - 4x^7 + 6x^6 - 4x^5 + x^4 by x2+1x^2+1, which yields:

x8−4x7+6x6−4x5+x4x2+1=x6−4x5+5x4−4x2+4−4x2+1\frac{x^8 - 4x^7 + 6x^6 - 4x^5 + x^4}{x^2+1} = x^6 - 4x^5 + 5x^4 - 4x^2 + 4 - \frac{4}{x^2+1}.

So the integral becomes:

I=∫01(x6−4x5+5x4−4x2+4−41+x2)dxI = \int_{0}^{1} \left( x^6 - 4x^5 + 5x^4 - 4x^2 + 4 - \frac{4}{1+x^2} \right) dx.

Integrating term by term:

∫01x6dx=17\int_{0}^{1} x^6 dx = \frac{1}{7}

∫01−4x5dx=−23\int_{0}^{1} -4x^5 dx = -\frac{2}{3}

∫015x4dx=1\int_{0}^{1} 5x^4 dx = 1

∫01−4x2dx=−43\int_{0}^{1} -4x^2 dx = -\frac{4}{3}

∫014dx=4\int_{0}^{1} 4 dx = 4

∫01−41+x2dx=−4arctan⁡(1)=−π\int_{0}^{1} -\frac{4}{1+x^2} dx = -4 \arctan(1) = -\pi

Summing these values:

I=17−23+1−43+4−π=17−63+5−π=17−2+5−π=17+3−π=227−πI = \frac{1}{7} - \frac{2}{3} + 1 - \frac{4}{3} + 4 - \pi = \frac{1}{7} - \frac{6}{3} + 5 - \pi = \frac{1}{7} - 2 + 5 - \pi = \frac{1}{7} + 3 - \pi = \frac{22}{7} - \pi.

Therefore, the value of the integral is 227−π\frac{22}{7} - \pi.