Question

The values of current $I$ flowing in a given resistor for corresponding values of potential difference $V$ across resistor are given below:

$I$ (Amperes)	$0.5$	$1$	$2$	$3$	$4$
$V$ (volts)	$1.6$	$3.4$	$6.7$	$10.2$	$13.2$

Plot the graph between $V$ and $I$ . Calculate the resistance of that resistor.

Answer 1

Hint : Here, the values of $I$ and $V$ are given and we have to plot these values in the graph and let us find the resistance by using the formula of $R = \dfrac{1}{{slope}}$ , resistance is the inverse of the slope of the graph between $I$ and $V$ .
Slope in the coordinate system is given by: $slope = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}$

Complete Step By Step Answer:
Here, let us first put the above given data in the graph such that take current $I$ on $x - axis$ and potential difference $V$ on $y - axis$ . As shown below:

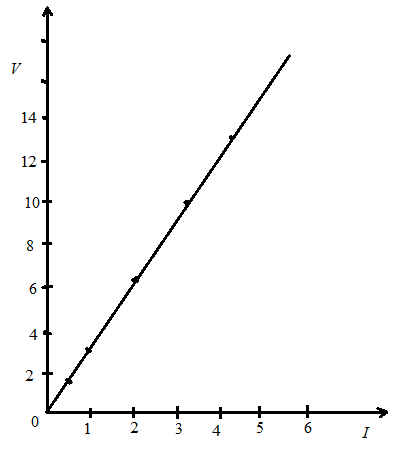
In the above figure we see a straight line between the current and potential difference. We know that if we have to find the slope of the straight line we have to consider any two points such that $(1,3.4)$ and $(3,10.2)$ .
Resistance is actually the inverse of the slope between the potential difference and current as:
$R = \dfrac{1}{{slope}}$ …. $(1)$
Let us first calculate the slope of the straight line as:
$slope = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}$
$\Rightarrow slope = \dfrac{{10.2 - 3.4}}{{3 - 1}}$ …. (We considered the points above)
$\Rightarrow slope = \dfrac{{6.8}}{2}$
$\therefore slope = 3.4$
So let us now put this value in equation $(1)$ and calculate resistance as:
$\therefore R = \dfrac{1}{{3.4}}$
$\Rightarrow R = 0.294\Omega$
Thus, we calculated the resistance of the above given data as $0.294\Omega$
Hence, we have obtained the answer.

Note :
We have plotted the graph as shown above and we know that the resistance is given by the inverse of the slope of the straight line between the potential difference and current. Calculate the terms carefully and write the decimal nos. precisely.