Question

The values of $\alpha$ if $(\alpha ,2\alpha )$lies inside the $\Delta ABC$ if
$A(0,2),B(2,0)$and $C(4,4)$
(a) $\alpha \in \left( \dfrac{1}{3},\dfrac{2}{3} \right)$
(b) $\alpha \in \left( \dfrac{2}{3},1 \right)$
(c) $\alpha \in \left( \dfrac{2}{3},\dfrac{4}{3} \right)$
(d) $\alpha \in \left( \dfrac{1}{3},1 \right)$

Answer 1

Hint: Find the equation of the lines which are forming the triangle.

The figure for the given problem is as follows:

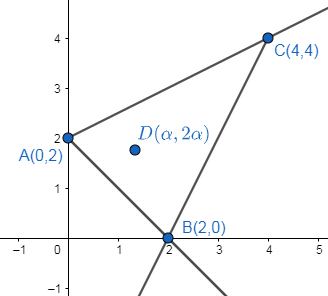
Now we will find the equations of all the three sides of the triangle.
We know equation of line between the two points $({{x}_{1}},{{y}_{1}})$ and $({{x}_{2}},{{y}_{2}})$can be written as,
$\dfrac{y-{{y}_{1}}}{{{y}_{2}}-{{y}_{1}}}=\dfrac{x-{{x}_{1}}}{{{x}_{2}}-{{x}_{1}}}$
Applying the above formula, the equation of side AB is,
$\dfrac{y-2}{0-2}=\dfrac{x-0}{2-0}$
$\dfrac{y-2}{-2}=\dfrac{x}{2}$
$\dfrac{y-2}{-1}=\dfrac{x}{1}$
On cross multiplication, we get
$y-2=-x$
$x+y-2=0........(i)$
Similarly, the equation of side BC is,
$\dfrac{y-0}{4-0}=\dfrac{x-2}{4-2}$
$\dfrac{y}{4}=\dfrac{x-2}{2}$
$\dfrac{y}{2}=\dfrac{x-2}{1}$
On cross multiplication, we get
$y=2x-4$
$2x-y-4=0........(ii)$
And, the equation of side AC is,
$\dfrac{y-2}{4-2}=\dfrac{x-0}{4-0}$
$\dfrac{y-2}{2}=\dfrac{x}{4}$
$\dfrac{y-2}{1}=\dfrac{x}{2}$
On cross multiplication, we get
$2y-4=x$
$x-2y+4=0........(iii)$
Therefore the figure with equations is,

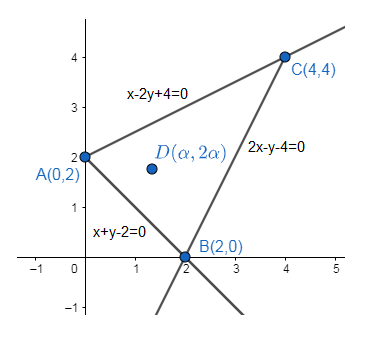
Two given points $\left( {{x}_{1}},\text{ }{{y}_{1}} \right)$and $\left( {{x}_{2}},\text{ }{{y}_{2}} \right)$will lie on the same side of the line $ax+by+c=0$ if $a{{x}_{1}}+b{{y}_{1}}+c$ and $a{{x}_{2}}+b{{y}_{2}}+c$ will have same signs.
From the above figure it is clear that the points B and D lie on the same side of the line AC. So, it should satisfy the above condition, i.e.,
$2-2(0)+4=6>0$
So, when we substitute the value of point D in line AC, it should be greater than zero, i.e.,
$\alpha -2(2\alpha )+4>0$
$\alpha -4\alpha +4>0$
$-3\alpha +4>0$
$4>3\alpha$
$\Rightarrow \alpha <\dfrac{4}{3}.........(iv)$
Now from the above figure it is clear that the points C and D lie on the same side of the line AB. Substitute value of point C in equation of line AB, we get
$4+4-2=6>0$
So, when we substitute the value of point D in line AB, it should be greater than zero, i.e.,
$\alpha +2\alpha -2>0$
$3\alpha -2>0$
$3\alpha >2$
$\Rightarrow \alpha >\dfrac{2}{3}.........(v)$
So, from equation (iv) and (v), we get
$\alpha \in \left( \dfrac{2}{3},\dfrac{4}{3} \right)$
Hence the correct answer is option (c).
Note: We can solve this by finding boundaries of x and y. But the options are given in fraction form, using this method it gives the exact answer.