Question

The values of $\alpha$ for which the point $\left( {\alpha - 1,\alpha + 1} \right)$ lies in the larger segment of the circle ${x^2} + {y^2} - x - y - 6 = 0$ made by the chord whose equation is x + y - 2 = 0 is
(a). -1 < $\alpha$ < 1
(b). 1 < $\alpha$< $\infty$
(c). -$\infty$ < $\alpha$< -1
(d). $\alpha \leqslant 0$

Answer 1

Using the given information from the question we can find the range of$\alpha$. That is substituting the given point in the equation of the circle, as the point lies on the circle. Using the condition that the point and the centre of the circle must have the same sign, we can get the values of $\alpha$. Using the inequalities we get, together we can form the value of $\alpha$.

Complete step-by-step answer :
The given circle S(x, y)$\equiv$ ${x^2} + {y^2} - x - y - 6 = 0$
On comparing the given equation with ${x^2} + {y^2} + 2gx + 2fy + c = 0$
We can decide 2g = -1 and 2f = -1 and c =-6
$\Rightarrow g = - \dfrac{1}{2}$
$\Rightarrow f = - \dfrac{1}{2}$
To find the centre of the circle, we have C = (-g, -f)
Centre at C$\equiv$ $\left( { - \left( { - \dfrac{1}{2}} \right), - \left( { - \dfrac{1}{2}} \right)} \right)$ $= \left( {\dfrac{1}{2},\dfrac{1}{2}} \right)$

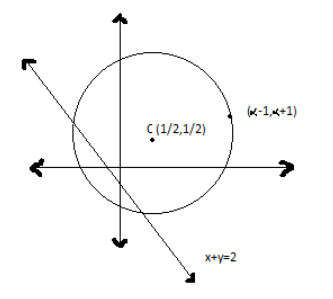
According to the given conditions, the given point P $\left( {\alpha - 1,\alpha + 1} \right)$ must lie inside the given circle.
i.e., S $\left( {\alpha - 1,\alpha + 1} \right) < 0$
That is, substitute the point in the given equation of circle ${x^2} + {y^2} - x - y - 6 = 0$
$\Rightarrow {\left( {\alpha - 1} \right)^2} + {\left( {\alpha + 1} \right)^2} - \left( {\alpha - 1} \right) - \left( {\alpha + 1} \right) - 6 < 0$
$\Rightarrow {\alpha ^2} - \alpha - 2 < 0$
$\Rightarrow \left( {\alpha - 2} \right)\left( {\alpha + 1} \right) < 0$
$\Rightarrow - 1 < \alpha < 2$… (2)
[Using sign-scheme from algebra]
And also Point P and Centre C must lie on the same side of the line.
Locus L(x, y) = x + y -2 = 0 … (3)
Locus: A shape created by the set of points whose points satisfies a given set of rules.
i.e., L $\left( {\dfrac{1}{2},\dfrac{1}{2}} \right)$and L$\left( {\alpha - 2} \right)\left( {\alpha + 1} \right)$ must have same sign.
Now, since L $\left( {\dfrac{1}{2},\dfrac{1}{2}} \right)$=$\dfrac{1}{2}$+$\dfrac{1}{2}$- 2 < 0
Therefore, we have
L$\left( {\alpha - 2} \right)\left( {\alpha + 1} \right)$=$\left( {\alpha - 1} \right) + (\alpha + 1) - 2 < 0$
$\Rightarrow \alpha < 1$… (4)
Inequalities (2) and (4) together give the permissible values of $\alpha$ as -1 < $\alpha$< 1

Note : Instead of asking the value of $\alpha$, we might be asked to find the number of integrals of $\alpha$. Then the solution or the integral value will be 0 and 1. Therefore the number of integral values will be 2. We can solve this by using graphical methods. We can plot and separate the integral points satisfying both the equations.