Question

The value of $|\vec{A}+\vec{B}-\vec{C}+\vec{D}|$ can be zero if :-

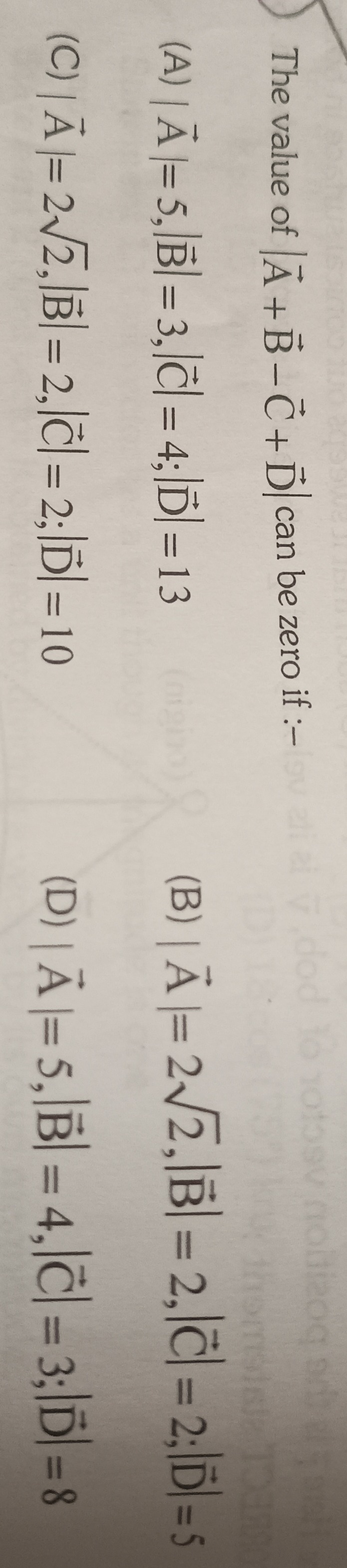
• A. $|\vec{A}|=5, |\vec{B}|=3, |\vec{C}|=4;|\vec{D}|=13
• B. $|\vec{A}|=2\sqrt{2}, |\vec{B}|=2, |\vec{C}|=2;|\vec{D}|=5
• C. $|\vec{A}|=2\sqrt{2}, |\vec{B}|=2, |\vec{C}|=2;|\vec{D}|=10
• D. $|\vec{A}|=5, |\vec{B}|=4, |\vec{C}|=3; |\vec{D}|=8

Answer 1

Answer: (B)

Option B: $|\vec{A}|=2\sqrt{2}, |\vec{B}|=2, |\vec{C}|=2;|\vec{D}|=5$

Answer 2

The value of $|\vec{A}+\vec{B}-\vec{C}+\vec{D}|$ can be zero if the vectors $\vec{A}$, $\vec{B}$, $-\vec{C}$, and $\vec{D}$ can be arranged to form a closed polygon. This means their vector sum is the zero vector:

$\vec{A}+\vec{B}-\vec{C}+\vec{D} = \vec{0}$

For four vectors with magnitudes $v_1, v_2, v_3, v_4$ to form a closed quadrilateral, the sum of the magnitudes of any three vectors must be greater than or equal to the magnitude of the fourth vector. Let the magnitudes of $\vec{A}, \vec{B}, \vec{C}, \vec{D}$ be $a, b, c, d$ respectively. The magnitudes of the four vectors in the sum are $|\vec{A}|=a$, $|\vec{B}|=b$, $|-\vec{C}|=c$, and $|\vec{D}|=d$.

The condition for these four magnitudes to form a closed quadrilateral is:

1. $a+b+c \ge d$
2. $a+b+d \ge c$
3. $a+c+d \ge b$
4. $b+c+d \ge a$

Checking option B: $|\vec{A}|=2\sqrt{2}, |\vec{B}|=2, |\vec{C}|=2, |\vec{D}|=5$.

$2\sqrt{2} + 2 + 2 \ge 5 \implies 2\sqrt{2} + 4 \ge 5 \implies 2\sqrt{2} \ge 1$ which is true.

$2\sqrt{2} + 2 + 5 \ge 2 \implies 2\sqrt{2} + 7 \ge 2$ which is true.

$2\sqrt{2} + 5 + 2 \ge 2 \implies 2\sqrt{2} + 7 \ge 2$ which is true.

$2 + 2 + 5 \ge 2\sqrt{2} \implies 9 \ge 2\sqrt{2}$ which is true.

All conditions are satisfied.

Note: Option D also satisfies the condition, which may indicate an error in the question or answer key.