Question
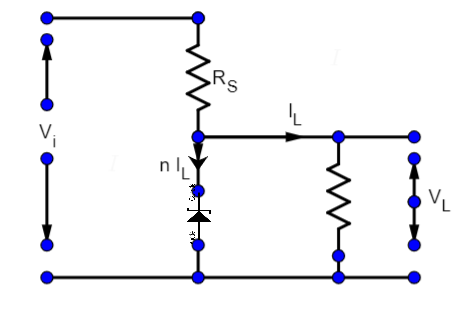
Question: The value of the resistor, \(R_S\), needed in the DC voltage regulator circuit shown here, equals: ...
The value of the resistor, RS, needed in the DC voltage regulator circuit shown here, equals:
(A) (n+1)ILVi+VL
(B) nILVi−VL
(C) nILVi+VL
(D) (n+1)ILVi−VL
Solution
We have to use Kirchhoff’s loop Law to calculate the value of the resistor RS . For this we will use the formula Vi−VL=IRS , where Vi is input voltage and VL is output voltage.
As we can see in figure the current I break down into two currents i.e. nIL,IL . So, we substitute these two values in the above equation.
After the substitution we will take the equation from both sides and find the value of RS.
Complete step by step solution
The given circuit is a zener diode circuit which is used as a voltage regulator. In this circuit Vi is unregulated input voltage and VL is regulated output voltage.
Now value of the resistor is calculated i.e. RS . For this we will use Kirchhoff's loop Law which states that the algebraic sum of all the potential differences along a closed loop in a circuit is zero.
So, the kirchhoff’s equation for the loop will be:
Vi−VL=IRS ,as voltage is equal to current ×resistance.
Where current, I=nIL+IL , as current I is broken into nIL,IL .
So the equation is Vi−VL=(nIL+IL)RS
By the above equation we can find RS
RS=(nIL+IL)Vi−VL
Now if we take IL common from the denominator in the above equation, then:
RS=(n+1)ILVi−VL .
So, option D is the correct option.
Note: The loop laws directly follow the fact that electrostatic force is a conservative force and the word done by it in any closed loop is zero.
While using Kirchhoff’s law also make sure that the positive negative sign is taken correctly, if it goes wrong the answer will be wrong.
Components are connected together in Series if the same current value flows throughout all the components. Components are connected together in Parallel if they have the same voltage across them.
