Question

The value of the resistance R in the figure is adjusted such that power dissipated in the resistor$2\,\Omega$ is maximum. Under this condition

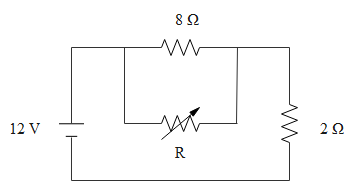
A. $R=0$
B. $R=8\Omega$
C. Power dissipated in the resistor $2\,\Omega$is 72 W.
D. Power dissipated in the resistor $2\,\Omega$is 8 W.

Answer 1

The equivalent resistance in the case of the resistors arranged in parallel will be less than the resistance of the smallest resistor, thus, the power dissipation will be maximum. The formula for computing the power dissipated is the square of the voltage by the resistance.
Formula used:
$P=\dfrac{{{V}^{2}}}{R}$

Complete answer:
From the given information, we have the data as follows.
The equivalent resistance in the case of the resistors arranged in parallel will be less than the resistance of the smallest resistor, thus, the power dissipation will be maximum. Similarly, the equivalent resistance in the case of the resistors arranged in series will be the sum of the resistance of the resistors, thus, the power dissipation will be minimal.
Thus, to avoid the maximum power dissipation in the parallel circuit R must be equal to zero. So, the equivalent resistance of the parallel resistors will be,

& {{R}_{p}}=\dfrac{0\times 8}{0+8} \\\ & \therefore {{R}_{p}}=0\Omega \\\ \end{aligned}$$ As the equivalent resistance equals zero, thus, the power dissipated in the resistor $$2\Omega $$ is given as follows. The formula for computing the power dissipated in terms of the voltage and the resistance is given as follows. $$P=\dfrac{{{V}^{2}}}{R}$$ Substitute the values in the above formula. $$\begin{aligned} & P=\dfrac{{{12}^{2}}}{2} \\\ & \therefore P=72\,W \\\ \end{aligned}$$ $$\therefore $$ The value of the power dissipated in the resistor $$2\,\Omega $$ is 72 W. **Thus, option (C) is correct.** **Note:** The equivalent resistance in the case of the resistors arranged in parallel will be less than the resistance of the smallest resistor, thus, the power dissipation will be maximum. Similarly, the equivalent resistance in the case of the resistors arranged in series will be the sum of the resistance of the resistors, thus, the power dissipation will be minimal.