Question
Question: The value of the $\lim_{n\to\infty} n\int_{0}^{\pi/4} \tan^n x \,dx$ is...
The value of the limn→∞n∫0π/4tannxdx is
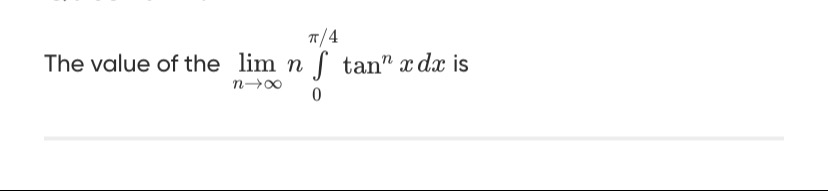
1/2
Solution
To evaluate the limit limn→∞n∫0π/4tannxdx, let In=∫0π/4tannxdx.
Step 1: Derive a recurrence relation for In.
We can relate In and In+2 using integration by parts or by manipulating the integrand.
Consider In+2:
In+2=∫0π/4tann+2xdx=∫0π/4tannx⋅tan2xdx
We know that tan2x=sec2x−1. Substitute this into the integral:
In+2=∫0π/4tannx(sec2x−1)dx In+2=∫0π/4tannxsec2xdx−∫0π/4tannxdx
The second term on the right is In.
For the first term, let u=tanx. Then du=sec2xdx.
When x=0, u=tan0=0. When x=π/4, u=tan(π/4)=1.
So, the first integral becomes:
∫01undu=[n+1un+1]01=n+11n+1−n+10n+1=n+11
Therefore, the recurrence relation is:
In+2=n+11−In
Rearranging this, we get:
In+In+2=n+11
Step 2: Show that limn→∞In=0.
For x∈[0,π/4), we have 0≤tanx<1. At x=π/4, tanx=1.
Let δ be a small positive number. We can split the integral:
In=∫0π/4−δtannxdx+∫π/4−δπ/4tannxdx
For the first integral, since 0≤x≤π/4−δ, we have 0≤tanx≤tan(π/4−δ). Let k=tan(π/4−δ). Since π/4−δ<π/4, we have k<1.
So, ∫0π/4−δtannxdx≤∫0π/4−δkndx=(π/4−δ)kn.
As n→∞, since k<1, kn→0. Thus, limn→∞∫0π/4−δtannxdx=0.
For the second integral, since π/4−δ≤x≤π/4, we have 0≤tanx≤1.
So, 0≤∫π/4−δπ/4tannxdx≤∫π/4−δπ/41ndx=∫π/4−δπ/41dx=π/4−(π/4−δ)=δ.
Since δ can be chosen arbitrarily small, this implies that limn→∞∫π/4−δπ/4tannxdx=0.
Therefore, limn→∞In=0.
Step 3: Evaluate the limit.
We have the recurrence relation In+In+2=n+11.
Multiply the entire equation by n:
nIn+nIn+2=n+1n
Now, take the limit as n→∞:
limn→∞(nIn+nIn+2)=limn→∞n+1n
Let L=limn→∞nIn.
The right-hand side limit is:
limn→∞n+1n=limn→∞1+1/n1=1+01=1
For the left-hand side, we have limn→∞nIn=L.
For the second term, limn→∞nIn+2:
nIn+2=n+2n⋅(n+2)In+2
As n→∞, limn→∞n+2n=limn→∞1+2/n1=1.
Also, limn→∞(n+2)In+2=L (since n+2 is just a shifted index, the limit value remains the same).
So, limn→∞nIn+2=1⋅L=L.
Substituting these limits back into the equation:
L+L=1 2L=1 L=21
The value of the limit is 1/2.
