Question
Question: The value of the integral $\int_0^{\pi/2} \frac{dx}{(1 + \sin^2 x)}$ lies in smallest interval out o...
The value of the integral ∫0π/2(1+sin2x)dx lies in smallest interval out of given options is:
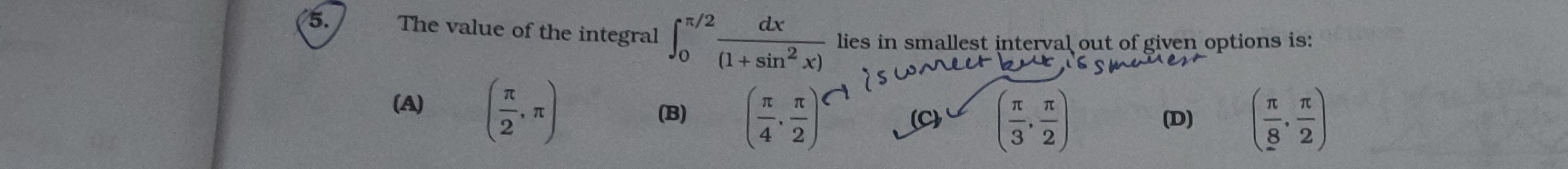
(2π,π)
(4π,2π)
(3π,2π)
(8π,2π)
(C)
Solution
To evaluate the integral I=∫0π/2(1+sin2x)dx, we follow these steps:
-
Transform the integrand: Divide the numerator and denominator by cos2x: I=∫0π/2(1+sin2x)/cos2x1/cos2xdx
I=∫0π/2sec2x+tan2xsec2xdx
Substitute sec2x=1+tan2x in the denominator:
I=∫0π/21+tan2x+tan2xsec2xdx
I=∫0π/21+2tan2xsec2xdx
-
Substitute and change limits: Let t=tanx. Then dt=sec2xdx.
When x=0, t=tan0=0.
When x=π/2, t=tan(π/2)→∞.
The integral becomes:
I=∫0∞1+2t2dt
-
Evaluate the transformed integral:
Factor out 2 from the denominator:
I=21∫0∞21+t2dt
Rewrite 21 as (21)2:
I=21∫0∞(21)2+t2dt
This is a standard integral of the form ∫a2+x2dx=a1arctan(ax). Here a=21.
I=21[1/21arctan(1/2t)]0∞
I=21[2arctan(2t)]0∞
I=22[arctan(2t)]0∞
I=21[arctan(∞)−arctan(0)]
I=21[2π−0]
I=22π
-
Simplify and compare with options:
The value of the integral is I=22π=4π2.
Now we need to find which of the given intervals contains this value and is the smallest.
Let's compare I with the bounds of the given intervals:
I=4π2≈43.14159×1.4142≈44.4428≈1.1107.
The options are:
(A) (2π,π)≈(1.5708,3.1416)
(B) (4π,2π)≈(0.7854,1.5708)
(C) (3π,2π)≈(1.0472,1.5708)
(D) (8π,2π)≈(0.3927,1.5708)
We need to check if I lies in these intervals more precisely.
Is I<2π?
22π<2π⟹21<1⟹1<2, which is true. So I is less than π/2.
Is I>3π?
22π>3π⟹221>31⟹3>22. Squaring both sides: 9>8, which is true. So I>π/3.
Therefore, I∈(3π,2π). This means option (C) contains I.
Since π/3>π/4>π/8, if I∈(π/3,π/2), then I must also be in (π/4,π/2) and (π/8,π/2).
So, options (B), (C), and (D) all contain the value of the integral.
We need to find the smallest interval among the given options that contains I. The "smallest" interval refers to the one with the shortest length.
Lengths of the intervals:
Length of (B) = 2π−4π=4π
Length of (C) = 2π−3π=6π
Length of (D) = 2π−8π=83π
Comparing the lengths: 6π<4π<83π (since 4/24<6/24<9/24).
The smallest length is 6π, which corresponds to interval (C).
