Question

The value of the integral $\int_{0}^{\infty} \frac{1}{x^4-x^2+1}dx$ is

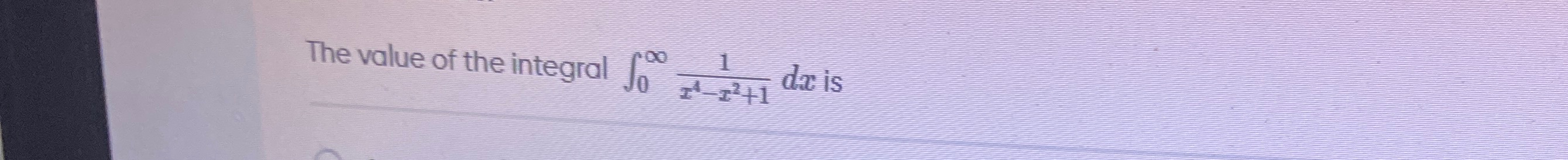
Answer 1

$\frac{\pi}{2}$

Answer 2

To evaluate the integral $I = \int_{0}^{\infty} \frac{1}{x^4-x^2+1}dx$, we can use a substitution and properties of definite integrals.

1. Symmetry Transformation: Apply the substitution $x = 1/t$ to the integral. This transforms the integral $\int_{0}^{\infty} \frac{1}{x^4-x^2+1}dx$ into $\int_{0}^{\infty} \frac{x^2}{x^4-x^2+1}dx$.
2. Summation: Add the original integral and the transformed integral. This yields $2I = \int_{0}^{\infty} \frac{1+x^2}{x^4-x^2+1}dx$.
3. Algebraic Manipulation: Divide the numerator and denominator of the integrand by $x^2$. This gives $2I = \int_{0}^{\infty} \frac{1/x^2+1}{x^2-1+1/x^2}dx$.
4. Substitution: Recognize that the denominator $x^2-1+1/x^2$ can be written as $(x-1/x)^2+1$, and the numerator $1/x^2+1$ is the differential of $x-1/x$. Let $u = x-1/x$. As $x$ goes from $0$ to $\infty$, $u$ goes from $-\infty$ to $\infty$.
5. Standard Integral: The integral simplifies to $2I = \int_{-\infty}^{\infty} \frac{du}{u^2+1}$.
6. Evaluation: Evaluate this standard integral, which is $[\arctan(u)]_{-\infty}^{\infty} = \pi/2 - (-\pi/2) = \pi$.
7. Final Result: Solve for $I$, giving $I = \pi/2$.