Question
Question: The value of the integral $\int_0^1 \sqrt{x + \sqrt{x + \sqrt{x + ...}}} dx$ is:...
The value of the integral ∫01x+x+x+...dx is:
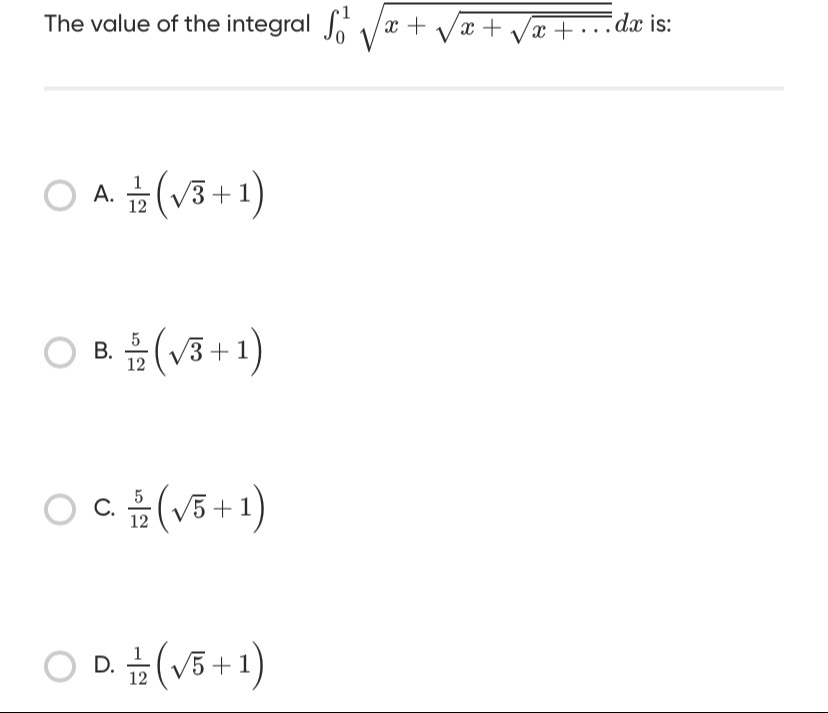
121(3+1)
125(3+1)
125(5+1)
121(5+1)
125(5+1)
Solution
To evaluate the integral ∫01x+x+x+...dx, we first need to simplify the expression inside the integral.
Let y=x+x+x+.... This is an infinite nested radical. We can express it as:
y=x+y
Now, square both sides of the equation:
y2=x+y
Rearrange the terms to form a quadratic equation in y:
y2−y−x=0
Solve for y using the quadratic formula y=2a−b±b2−4ac, where a=1, b=−1, and c=−x:
y=2(1)−(−1)±(−1)2−4(1)(−x)
y=21±1+4x
Since y represents a square root, it must be non-negative. The term 1+4x is always positive for x≥0. If we take the minus sign, 1−1+4x would be negative (because 1+4x>1 for x>0). Therefore, we must choose the positive root:
y=21+1+4x
Now, substitute this expression for y back into the integral:
I=∫0121+1+4xdx
We can factor out 21 and split the integral:
I=21∫01(1+1+4x)dx
I=21[∫011dx+∫01(1+4x)1/2dx]
Evaluate each integral separately:
-
∫011dx=[x]01=1−0=1
-
∫01(1+4x)1/2dx
To integrate this, use a substitution. Let u=1+4x. Then du=4dx, which means dx=41du.
Change the limits of integration:
When x=0, u=1+4(0)=1.
When x=1, u=1+4(1)=5.
The integral becomes:
∫15u1/241du=41∫15u1/2du
=41[3/2u3/2]15
=41[32u3/2]15
=61[u3/2]15
=61(53/2−13/2)
=61(55−1)
Now, substitute these results back into the expression for I:
I=21[1+61(55−1)]
I=21[66+655−1]
I=21[66+55−1]
I=21[65+55]
I=125+55
I=125(1+5)
Comparing this result with the given options, it matches option C.
