Question
Question: The value of the integral $\int_{0}^{1} \frac{x^3+x+1}{3x^2-3x+4} dx$ is...
The value of the integral ∫013x2−3x+4x3+x+1dx is
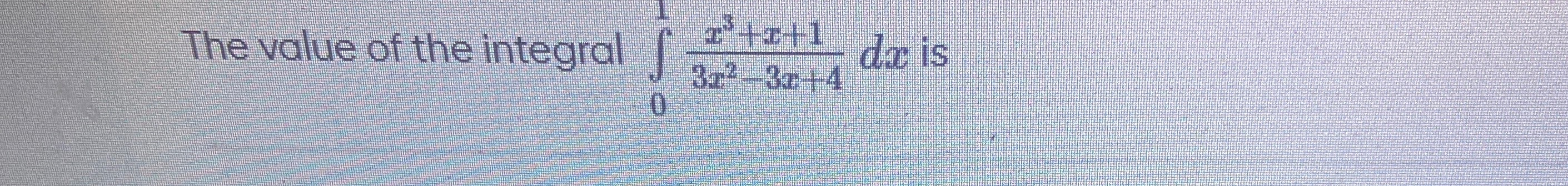
1/2
Solution
To evaluate the integral ∫013x2−3x+4x3+x+1dx, we first perform polynomial long division because the degree of the numerator (3) is greater than the degree of the denominator (2).
Step 1: Polynomial Long Division
Divide x3+x+1 by 3x2−3x+4:
So, we can write the integrand as: 3x2−3x+4x3+x+1=31x+31+3x2−3x+432x−31 =31x+31+3(3x2−3x+4)2x−1
Step 2: Split the Integral
Now, we can split the integral into two parts: I=∫01(31x+31)dx+∫013(3x2−3x+4)2x−1dx Let I1=∫01(31x+31)dx and I2=∫013(3x2−3x+4)2x−1dx.
Step 3: Evaluate I1
I1=[312x2+31x]01 I1=[6x2+3x]01 I1=(612+31)−(602+30) I1=61+62−0=63=21
Step 4: Evaluate I2
I2=31∫013x2−3x+42x−1dx Let u=3x2−3x+4. Then, du=(6x−3)dx=3(2x−1)dx. So, (2x−1)dx=31du.
Now, change the limits of integration for u: When x=0, u=3(0)2−3(0)+4=4. When x=1, u=3(1)2−3(1)+4=3−3+4=4.
Substitute u and du into the integral I2: I2=31∫44u31du I2=91∫44u1du Since the upper and lower limits of integration are the same, the value of the definite integral is 0. I2=0.
Step 5: Combine the Results
The total integral I=I1+I2. I=21+0=21.
The final answer is 21.
Explanation of the solution:
The integral is evaluated by first performing polynomial long division to simplify the integrand. This splits the integral into two parts: a simple polynomial and a rational function. The polynomial part is integrated directly. The rational function part is integrated using a substitution where the numerator is a multiple of the derivative of the denominator. A key observation is that the limits of integration for the substituted variable become identical, making the second part of the integral zero.
Answer:
The value of the integral is 21.
