Question

The value of the integral $\iint{xy\left( x+y \right)dxdy}$ over the area between $y={{x}^{2}}\And y=x$ is:
(a) $\dfrac{3}{56}$
(b) $\dfrac{47}{56}$
(c) $\dfrac{33}{56}$
(d) $\dfrac{23}{56}$

Answer 1

First of all draw the figure of the two curves $y={{x}^{2}}\And y=x$ and then find the area between these two curves and write the end points of this area. Then integrate the given integral $\iint{xy\left( x+y \right)dxdy}$ by first of all keeping x as constant and integrating y. Then put the limits of y. After that integrate the expression with respect to x and apply the limits of x.

Complete step-by-step answer:
First of all, we are going to draw the two curves $y={{x}^{2}}\And y=x$ in the same graph.

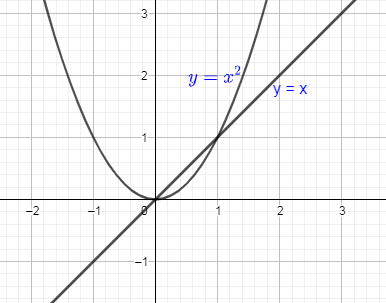
Now, we are going to shade the area between these two curves and also will mark the end points.

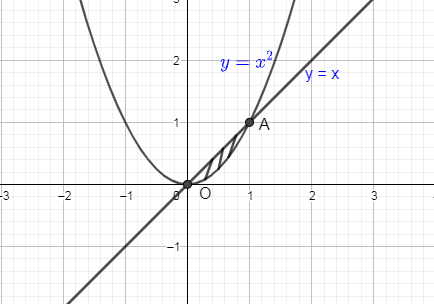
From the figure, we got the lower and upper limit of x is 0 and 1 respectively. And we got the lower and the upper limit of y as x and ${{x}^{2}}$ respectively.
Now, integrating the given integral we get,
$\iint{xy\left( x+y \right)dxdy}$
First of all, we are taking x as constant then the above integral will look like:
$\begin{aligned} & \int{\left( \int{\left( x\left( xy+{{y}^{2}} \right) \right)dy} \right)}dx \\\ & \Rightarrow \int{\left( \int{x\left( xy \right)dy+\int{x{{y}^{2}}dy}} \right)}dx \\\ \end{aligned}$
We know the integration of ${{y}^{n}}$ with respect to y as follows:
$\int{{{y}^{n}}}dy=\dfrac{{{y}^{n+1}}}{n+1}$
Applying the above integration property in the above integration we get,
$\int{\left( \left( \dfrac{{{x}^{2}}{{y}^{2}}}{2} \right)+\dfrac{x{{y}^{3}}}{3} \right)}dx$
And putting the lower and the upper limit of y as ${{x}^{2}}$and x respectively in the above integral and we get,

& \int{\left( \left( \dfrac{{{x}^{2}}{{y}^{2}}}{2} \right)+\dfrac{x{{y}^{3}}}{3} \right)}_{{{x}^{2}}}^{x}dx \\\ & \Rightarrow \int{\left( \left[ \dfrac{{{x}^{2}}{{\left( x \right)}^{2}}}{2}+\dfrac{x{{\left( x \right)}^{3}}}{3} \right]-\left[ \dfrac{{{x}^{2}}{{\left( {{x}^{2}} \right)}^{2}}}{2}+\dfrac{x{{\left( {{x}^{2}} \right)}^{3}}}{3} \right] \right)}dx \\\ \end{aligned}$$ $$\begin{aligned} & \Rightarrow \int{\left( \left[ \dfrac{{{x}^{4}}}{2}+\dfrac{{{x}^{4}}}{3} \right]-\left[ \dfrac{{{x}^{6}}}{2}+\dfrac{{{x}^{7}}}{3} \right] \right)dx} \\\ & \Rightarrow \int{\left( \left[ \dfrac{5{{x}^{4}}}{6} \right]-\left[ \dfrac{{{x}^{6}}}{2}+\dfrac{{{x}^{7}}}{3} \right] \right)dx} \\\ \end{aligned}$$ Now, integrating the above integral with respect to x we get, $\dfrac{5{{x}^{5}}}{6\left( 5 \right)}-\dfrac{{{x}^{7}}}{2\left( 7 \right)}-\dfrac{{{x}^{8}}}{3\left( 8 \right)}$ Applying the lower and upper limit as 0 and 1 respectively in the above expression we get, $\begin{aligned} & \left( \dfrac{5{{x}^{5}}}{6\left( 5 \right)}-\dfrac{{{x}^{7}}}{2\left( 7 \right)}-\dfrac{{{x}^{8}}}{3\left( 8 \right)} \right)_{0}^{1} \\\ & \Rightarrow \dfrac{5{{\left( 1 \right)}^{5}}}{6\left( 5 \right)}-\dfrac{{{\left( 1 \right)}^{7}}}{2\left( 7 \right)}-\dfrac{{{\left( 1 \right)}^{8}}}{3\left( 8 \right)} \\\ & \Rightarrow \dfrac{1}{6}-\dfrac{1}{14}-\dfrac{1}{24}-0 \\\ \end{aligned}$ Taking 168 as L.C.M in the denominator and we get, $\begin{aligned} & \dfrac{28-12-7}{168} \\\ & =\dfrac{28-19}{168} \\\ & =\dfrac{9}{168} \\\ \end{aligned}$ The numerator and the denominator in the above expression will be divisible by 3 and we get, $\dfrac{3}{56}$ From the above, we got the result of the integral over the area between the given curves is $\dfrac{3}{56}$. **So, the correct answer is “Option (a)”.** **Note:** In this problem, we have learnt a very important concept how to integrate the integral having two variables in it. Also, the mistake that could be possible is the calculation mistake when doing the integration by keeping x as constant and then keeping y as constant.