Question

The value of the given expression $\sin \left( {{\tan }^{-1}}x \right)\,,\,\left| \left. x \right|<1 \right.$ is equal to
(a) $\dfrac{x}{\sqrt{1-{{x}^{2}}}}$
(b) $\dfrac{1}{\sqrt{1-{{x}^{2}}}}$
(c) $\dfrac{1}{\sqrt{1+{{x}^{2}}}}$
(d) $\dfrac{x}{\sqrt{1+{{x}^{2}}}}$

Answer 1

Hint: First, we will consider a right angled triangle with base as 1 unit, perpendicular of x units and hypotenuse of y units. We will then apply the Pythagoras theorem to find the third side of the triangle and we will also apply the trigonometric formula given by $\sin \left( {{\sin }^{-1}}\left( q \right) \right)=q$.

Complete step-by-step answer:
We will first consider the expression given as $\sin \left( {{\tan }^{-1}}x \right)\,,\,\left| \left. x \right|<1 \right.$. We will convert the inverse tan term into inverse sine term. For that we will substitute ${{\tan }^{-1}}x=a$. Now we will place inverse tan to the right side of the equation. Therefore, we have $x=\tan \left( a \right)$.
At this step we will apply the formula $\tan \left( p \right)=\dfrac{\text{perpendicular}}{\text{Base}}$. By comparing $x=\tan \left( a \right)$ and $\tan \left( p \right)=\dfrac{\text{perpendicular}}{\text{Base}}$ we come to know that perpendicular is x units and base is 1 unit. This is because $x=\tan \left( a \right)$ can also be written as $\dfrac{x}{1}=\tan \left( a \right)$. Therefore, the diagram for the given question is shown below.

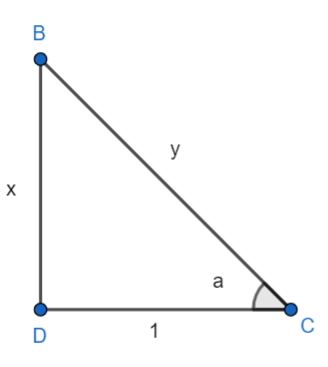
Now we will apply Pythagoras theorem to the right angled triangle at D. This results into $\begin{aligned} & {{y}^{2}}={{x}^{2}}+{{\left( 1 \right)}^{2}} \\\ & \Rightarrow {{y}^{2}}={{x}^{2}}+1 \\\ \end{aligned}$
By taking square roots on both the sides of the equation we will have ${{y}^{2}}={{x}^{2}}+1$ as $y=\pm \sqrt{{{x}^{2}}+1}$. As we know that the side of the triangle cannot be negative so we get the value of $y=\sqrt{{{x}^{2}}+1}$ which is the hypotenuse of the triangle.
Now we will apply the formula $\sin \left( p \right)=\dfrac{\text{Perpendicular}}{\text{Hypotenuse}}$. As we can clearly see that the perpendicular of the triangle is x units and we know that the value of hypotenuse is $\sqrt{{{x}^{2}}+1}$.
Therefore, we have $\sin \left( a \right)=\dfrac{x}{\sqrt{{{x}^{2}}+1}}$. By placing the sine operation to the right side of the equation we will get $a={{\sin }^{-1}}\left( \dfrac{x}{\sqrt{{{x}^{2}}+1}} \right)$.
As we know that ${{\tan }^{-1}}x=a$ so, by comparing it to the term $a={{\sin }^{-1}}\left( \dfrac{x}{\sqrt{{{x}^{2}}+1}} \right)$ will result into ${{\tan }^{-1}}x={{\sin }^{-1}}\left( \dfrac{x}{\sqrt{{{x}^{2}}+1}} \right)$. Now we will substitute this in expression $\sin \left( {{\tan }^{-1}}x \right)\,,\,\left| \left. x \right|<1 \right.$.
Therefore, we have $\sin \left( {{\tan }^{-1}}x \right)\,=\sin \left( {{\sin }^{-1}}\left( \dfrac{x}{\sqrt{{{x}^{2}}+1}} \right) \right)$. Now we will apply the formula $\sin \left( {{\sin }^{-1}}\left( q \right) \right)=q$ therefore, we get $\sin \left( {{\tan }^{-1}}x \right)\,=\dfrac{x}{\sqrt{{{x}^{2}}+1}}$ which is the required value.
Hence, the correct option is (d).

Note: The value of the expression that we have got has a restriction of x as $\left| \left. x \right|<1 \right.$. Alternative method for this question is that we can also use the formula $\cos \left( p \right)=\dfrac{\text{Base}}{\text{Hypotenuse}}$ and after that apply the formula ${{\sin }^{2}}\left( p \right)+{{\cos }^{2}}\left( p \right)=1$ to find the value of $\sin \left( a \right)=\dfrac{x}{\sqrt{{{x}^{2}}+1}}$.