Question

The value of the focal length of the lens is equal to the value of the image distance when rays are
(A) Passing through optical center
(B) Parallel to the principal axis.
(C) Passing through focus.
(D) Over the mirror

Answer 1

Hint
Distance of focus from the optical center is equal to the distance of the image from the optical center. We have to find the situation then this condition is possible. We will draw a ray diagram and use lens formula to find the behavior of rays for this image formation.

Complete step by step answer

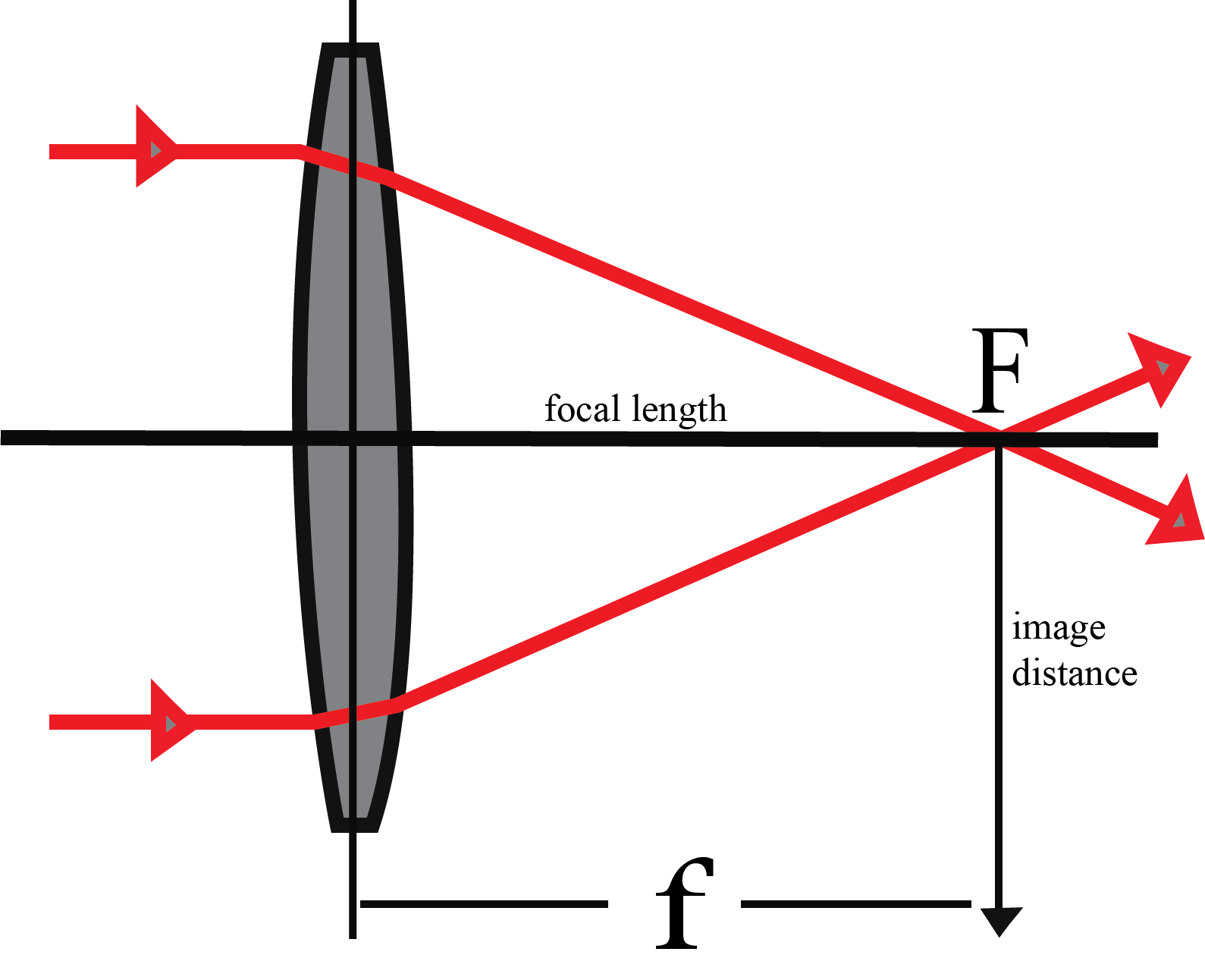
Focal length: distance between focus and optical center.
Image distance: distance between image and optical center.
Optical center: central point of spherical surface is the center of the lens both in concave as well as convex lens.
Len’s formula
$\Rightarrow \dfrac{1}{f} = \dfrac{1}{v} + \dfrac{1}{u}$ …(1)
Where f = focal length of lens
v= image distance
o= object distance
Lens formula is the same for concave lenses as well as for convex lenses.
It is mention in question that focal length = image distance or f=v …(2)
Using equation (2) in (1), we get
$\Rightarrow \dfrac{1}{f} = \dfrac{1}{f} + \dfrac{1}{u}$
$\Rightarrow \dfrac{1}{f} - \dfrac{1}{f} = \dfrac{1}{u}$
$\Rightarrow \dfrac{1}{u} = 0$
$\Rightarrow u = \infty$
Rays are coming from infinity and will pass through focus. This shows that the object is placed at infinity.
Let us draw a ray diagram of image formation by convex lens.
When an object is placed at infinity, a parallel beam strikes the lens and will pass through focus. Rays coming from center will follow the same path. Hence an inverted image is formed.
Option (B) is correct.

Note
If the object is placed at focus then no image is obtained. But in our case the image formed at a distance which is equal to focal length. So, we cannot place an object anywhere because it is at some point in infinity.