Question
Question: The value of $\tan^{-1}\left[\frac{\sqrt{1+x^2}+\sqrt{1-x^2}}{\sqrt{1+x^2}-\sqrt{1-x^2}}\right], |x|...
The value of tan−1[1+x2−1−x21+x2+1−x2],∣x∣≤21,x=0, is equal to [JEE(Main)-2017]
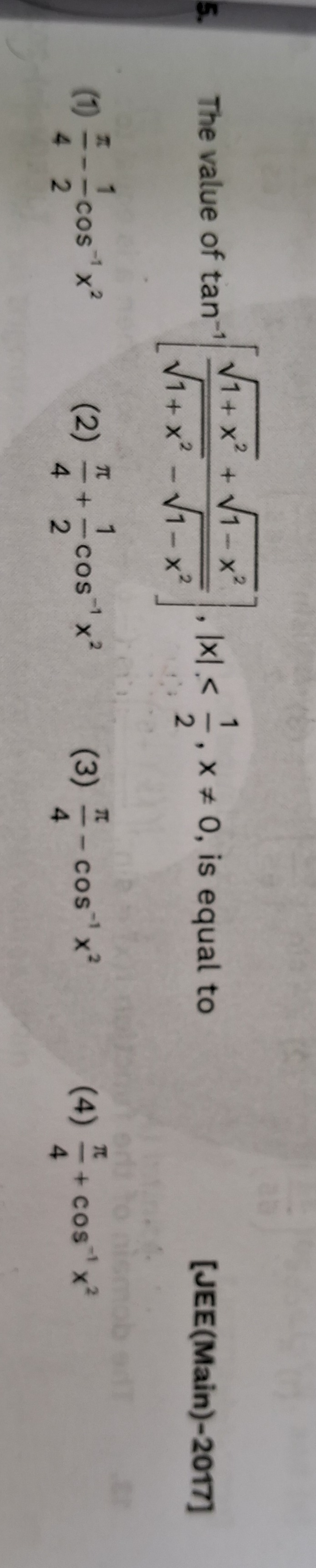
4π−21cos−1x2
4π+21cos−1x2
4π−cos−1x2
4π+cos−1x2
4π+21cos−1x2
Solution
Let the given expression be y. y=tan−1[1+x2−1−x21+x2+1−x2]
The domain is given as ∣x∣≤21, x=0. Squaring the inequality, we get x2≤21. Since x=0, x2=0. Also, x2≥0 for real x. Thus, 0<x2≤21.
Let's make the substitution x2=cosθ. Since 0<x2≤21, we have 0<cosθ≤21. As x2≥0, cosθ≥0. The range of θ=cos−1(x2) for x2∈(0,1/2] is [cos−1(1/2),cos−1(0)), which is [3π,2π).
Now substitute x2=cosθ into the expression: y=tan−1[1+cosθ−1−cosθ1+cosθ+1−cosθ] Using the half-angle identities 1+cosθ=2cos2(θ/2) and 1−cosθ=2sin2(θ/2): 1+cosθ=2cos2(θ/2)=2∣cos(θ/2)∣ 1−cosθ=2sin2(θ/2)=2∣sin(θ/2)∣
The range of θ is [3π,2π). The range of θ/2 is [6π,4π). In this range, both cos(θ/2) and sin(θ/2) are positive. So, ∣cos(θ/2)∣=cos(θ/2) and ∣sin(θ/2)∣=sin(θ/2).
Substituting these into the expression for y: y=tan−1[2cos(θ/2)−2sin(θ/2)2cos(θ/2)+2sin(θ/2)] y=tan−1[cos(θ/2)−sin(θ/2)cos(θ/2)+sin(θ/2)]
To simplify the expression inside the tan−1, divide the numerator and the denominator by cos(θ/2): y=tan−1[cos(θ/2)cos(θ/2)−cos(θ/2)sin(θ/2)cos(θ/2)cos(θ/2)+cos(θ/2)sin(θ/2)] y=tan−1[1−tan(θ/2)1+tan(θ/2)]
This expression is in the form 1−tanA1+tanA, which is the expansion of tan(4π+A). So, y=tan−1[tan(4π+2θ)].
Now we need to evaluate tan−1(tan(ϕ)). This is equal to ϕ if ϕ is in the principal value range of tan−1, which is (−2π,2π). The range of θ/2 is [6π,4π). The range of 4π+2θ is [4π+6π,4π+4π). 4π+6π=123π+2π=125π. 4π+4π=42π=2π. So the range of 4π+2θ is [125π,2π). This interval [125π,2π) is a subset of the principal value range (−2π,2π). Therefore, y=4π+2θ.
Substitute back θ in terms of x2. We used x2=cosθ, so θ=cos−1(x2). y=4π+2cos−1(x2).
Comparing this result with the given options, our result matches option (2).
The final answer is 4π+21cos−1x2.
