Question
Question: The value of $\tan^{-1} \left[ \frac{1}{4\sqrt{3}} \sum_{n=0}^{10} \frac{1}{\cos(\frac{7\pi}{12}+\fr...
The value of tan−1[431∑n=010cos(127π+2nπ)cos(127π+2(n+1)π)1] in the interval (−2π,2π) equals
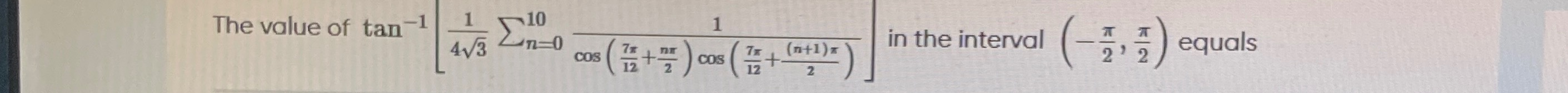
6π
Solution
Let the given expression be E. E=tan−1[431∑n=010cos(127π+2nπ)cos(127π+2(n+1)π)1].
Let θn=127π+2nπ. The general term of the sum is cos(θn)cos(θn+1)1. We have θn+1−θn=(127π+2(n+1)π)−(127π+2nπ)=2π.
Consider the identity tan(B)−tan(A)=cos(A)cos(B)sin(B−A). Let A=θn and B=θn+1. Then B−A=2π. sin(B−A)=sin(2π)=1. So, tan(θn+1)−tan(θn)=cos(θn)cos(θn+1)1.
The sum is a telescoping series: S=∑n=010cos(θn)cos(θn+1)1=∑n=010(tan(θn+1)−tan(θn)). S=(tan(θ1)−tan(θ0))+(tan(θ2)−tan(θ1))+⋯+(tan(θ11)−tan(θ10)). S=tan(θ11)−tan(θ0).
We need to calculate θ0 and θ11. θ0=127π+20π=127π. θ11=127π+211π=127π+1266π=1273π.
Now we calculate tan(θ0) and tan(θ11). tan(θ0)=tan(127π)=tan(123π+124π)=tan(4π+3π). Using the formula tan(A+B)=1−tanAtanBtanA+tanB: tan(127π)=1−tan(π/4)tan(π/3)tan(π/4)+tan(π/3)=1−1⋅31+3=1−31+3. Multiply numerator and denominator by 1+3: tan(127π)=(1−3)(1+3)(1+3)2=1−31+3+23=−24+23=−2−3.
tan(θ11)=tan(1273π). 1273π=1272π+π=6π+12π. Using the property tan(nπ+x)=tan(x) for integer n: tan(1273π)=tan(6π+12π)=tan(12π). tan(12π)=tan(15∘)=tan(45∘−30∘). Using the formula tan(A−B)=1+tanAtanBtanA−tanB: tan(12π)=1+tan(45∘)tan(30∘)tan(45∘)−tan(30∘)=1+1⋅311−31=33+133−1=3+13−1. Multiply numerator and denominator by 3−1: tan(12π)=(3+1)(3−1)(3−1)2=3−13+1−23=24−23=2−3.
The sum S=tan(θ11)−tan(θ0)=(2−3)−(−2−3)=2−3+2+3=4.
The expression inside the inverse tangent is 431⋅S=431⋅4=31.
We need to find the value of tan−1(31) in the interval (−2π,2π). The principal value of tan−1(31) is 6π. Since −2π<6π<2π, the value is 6π.
