Question

The value of $\sum_{r=0}^{2024} (-1)^r {^{2024}C_r} (2024-r)^{2024}$

Answer 1

2024!

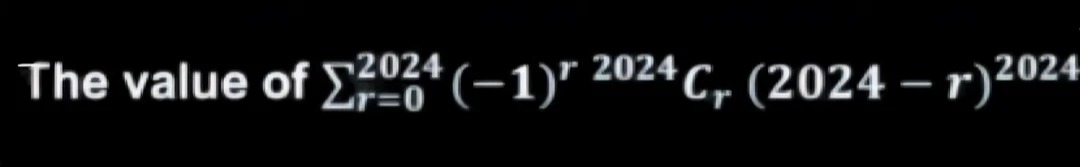
Answer 2

The given sum is $\sum_{r=0}^{2024} (-1)^r {^{2024}C_r} (2024-r)^{2024}$.

Let $n=2024$. The sum becomes $\sum_{r=0}^{n} (-1)^r {^nC_r} (n-r)^n$.

Change the index of summation from $r$ to $k=n-r$. When $r=0$, $k=n$. When $r=n$, $k=0$. Also, $r=n-k$.

The sum transforms to $\sum_{k=n}^{0} (-1)^{n-k} {^nC_{n-k}} k^n$.

Since ${^nC_{n-k}} = {^nC_k}$, and reversing the summation order, we get: $\sum_{k=0}^{n} (-1)^{n-k} {^nC_k} k^n$.

This is a standard combinatorial identity, which equals $n!$.

This identity represents the $n$-th forward difference of $x^n$ evaluated at $x=0$, i.e., $\Delta^n x^n |_{x=0} = n!$.

It also represents the number of surjective functions from a set of $n$ elements to a set of $n$ elements, which is $n!$.

Substituting $n=2024$, the value of the sum is $2024!$.