Question

The value of $\sum_{m=1}^{n} tan^{-1}(\frac{2m}{m^4+m^2+2})$ is:

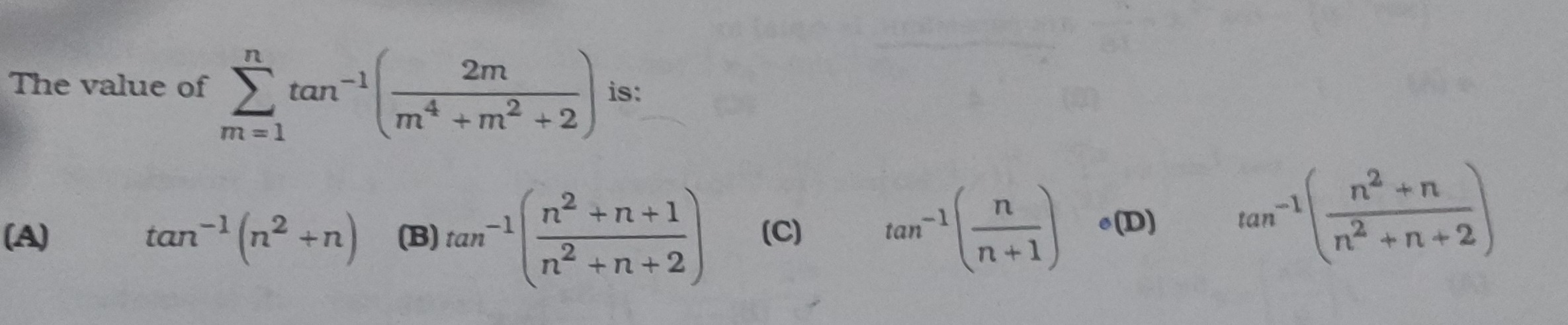
• A. $tan^{-1}(n^2+n)$
• B. $tan^{-1}(\frac{n^2+n+1}{n^2+n+2})$
• C. $tan^{-1}(\frac{n}{n+1})$
• D. $tan^{-1}(\frac{n^2+n}{n^2+n+2})$

Answer 1

Answer: (D)

tan^{-1}(\frac{n^2+n}{n^2+n+2})

Answer 2

The given series term $tan^{-1}(\frac{2m}{m^4+m^2+2})$ is transformed using the identity $tan^{-1}(X) - tan^{-1}(Y) = tan^{-1}(\frac{X-Y}{1+XY})$.

The denominator $m^4+m^2+2$ is rewritten as $1+(m^2-m+1)(m^2+m+1)$.

The numerator $2m$ is the difference $(m^2+m+1) - (m^2-m+1)$.

Thus, the general term becomes $tan^{-1}(m^2+m+1) - tan^{-1}(m^2-m+1)$.

This is a telescoping series. When summed from $m=1$ to $n$, most terms cancel out, leaving $tan^{-1}(n^2+n+1) - tan^{-1}(1)$.

Applying the $tan^{-1}(X) - tan^{-1}(Y)$ identity again with $X=n^2+n+1$ and $Y=1$, we get $tan^{-1}(\frac{n^2+n}{n^2+n+2})$.