Question
Question: The value of $\sqrt{\pi \int_0^{2008} x|\sin \pi x|dx}$ is equal to...
The value of π∫02008x∣sinπx∣dx is equal to
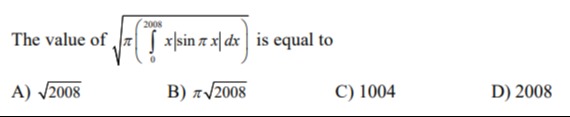
2008
π2008
1004
2008
2008
Solution
To find the value of π∫02008x∣sinπx∣dx, we first need to evaluate the integral I=∫02008x∣sinπx∣dx.
The function ∣sinπx∣ is periodic with period 1. We can split the integral over the intervals [n,n+1] for n=0,1,…,2007. I=∑n=02007∫nn+1x∣sinπx∣dx.
Let's consider the integral over a single interval [n,n+1]. Let x=n+u, so dx=du. When x=n, u=0. When x=n+1, u=1. ∫nn+1x∣sinπx∣dx=∫01(n+u)∣sinπ(n+u)∣du. We have sinπ(n+u)=sin(nπ+πu)=sin(nπ)cos(πu)+cos(nπ)sin(πu)=(−1)nsin(πu). So, ∣sinπ(n+u)∣=∣(−1)nsin(πu)∣=∣sin(πu)∣. For u∈[0,1], πu∈[0,π], so sin(πu)≥0. Thus, ∣sin(πu)∣=sin(πu). The integral becomes ∫01(n+u)sin(πu)du. We can split this into two integrals: ∫01nsin(πu)du+∫01usin(πu)du.
First integral: n∫01sin(πu)du=n[−πcos(πu)]01=n(−πcos(π)−(−πcos(0)))=n(−π−1+π1)=n(π1+π1)=π2n.
Second integral: ∫01usin(πu)du. We use integration by parts: ∫vdw=vw−∫wdv. Let v=u and dw=sin(πu)du. Then dv=du and w=∫sin(πu)du=−πcos(πu). ∫01usin(πu)du=[−πucos(πu)]01−∫01(−πcos(πu))du =(−π1cos(π)−(−π0cos(0)))+π1∫01cos(πu)du =π1+π1[πsin(πu)]01 =π1+π21(sin(π)−sin(0))=π1+π21(0−0)=π1.
So, ∫nn+1x∣sinπx∣dx=π2n+π1=π2n+1.
Now, we sum this expression from n=0 to n=2007: I=∑n=02007π2n+1=π1∑n=02007(2n+1). The sum ∑n=02007(2n+1)=1+3+5+⋯+(2×2007+1)=1+3+5+⋯+4015. This is the sum of the first 2008 odd numbers. The sum of the first N odd numbers is N2. Here, N=2008. So the sum is 20082.
So, I=π1×20082.
The question asks for the value of πI. πI=π×(π1×20082)=20082. Since 2008 is a positive number, 20082=2008.
