Question

The value of $(\sqrt{5}+1)^5-(\sqrt{5}-1)^5$ is

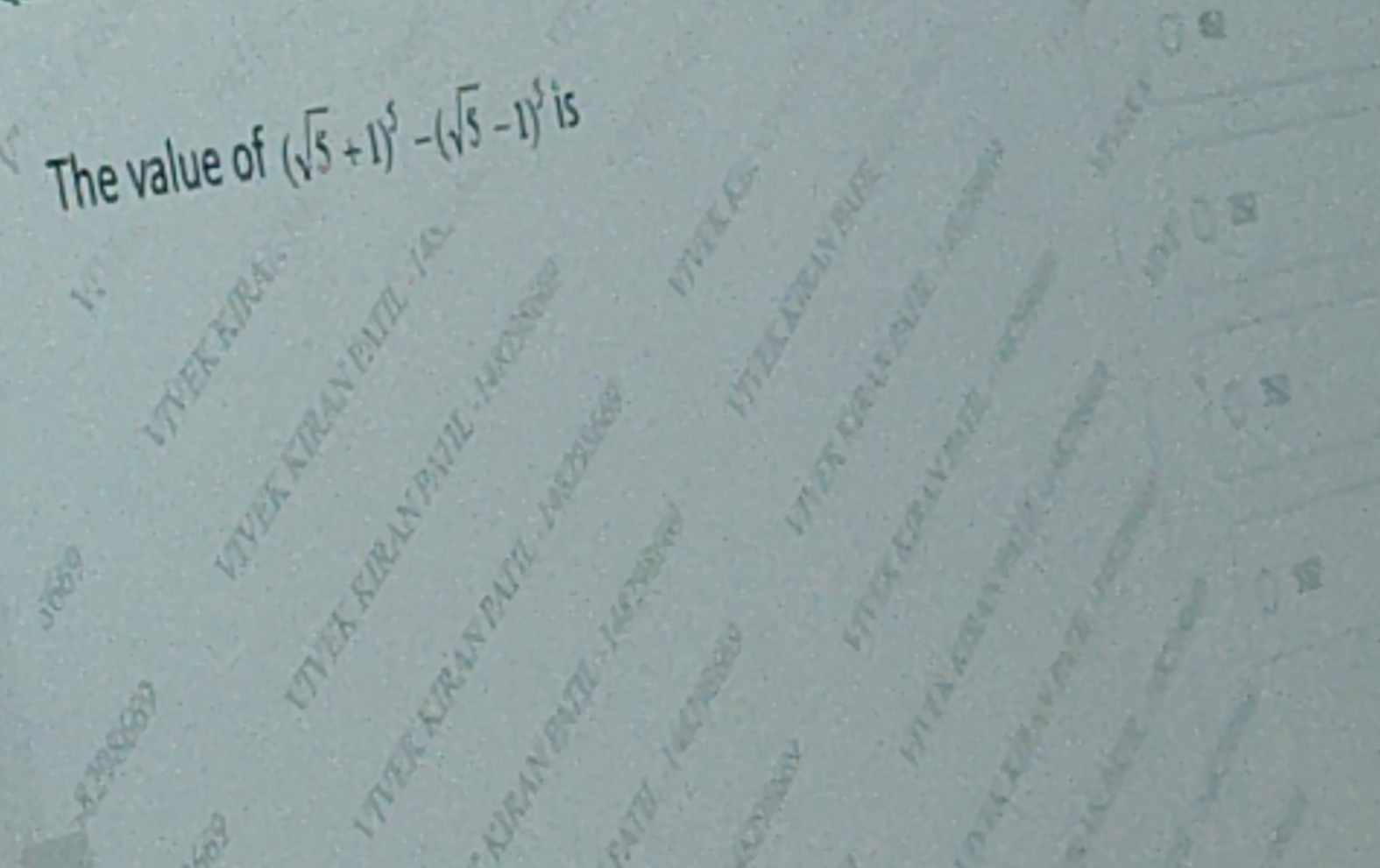
Answer 1

352

Answer 2

Let $x = \sqrt{5}$ and $y = 1$. The expression is $(x+y)^5 - (x-y)^5$.

Using the binomial theorem: $(x+y)^5 = x^5 + 5x^4y + 10x^3y^2 + 10x^2y^3 + 5xy^4 + y^5$ $(x-y)^5 = x^5 - 5x^4y + 10x^3y^2 - 10x^2y^3 + 5xy^4 - y^5$

Subtracting the second from the first: $(x+y)^5 - (x-y)^5 = 2(5x^4y + 10x^2y^3 + y^5)$ $= 10x^4y + 20x^2y^3 + 2y^5$

Substitute $x = \sqrt{5}$ and $y = 1$: $= 10(\sqrt{5})^4(1) + 20(\sqrt{5})^2(1)^3 + 2(1)^5$ $= 10(25)(1) + 20(5)(1) + 2(1)$ $= 250 + 100 + 2$ $= 352$