Question

The value of $\sin {\left( {231} \right)^ \circ }$ is equivalent to
A) $\cos {39^ \circ }$
B) $- \cos {39^ \circ }$
C) $- \sin {39^ \circ }$
D) $\sin {39^ \circ }$
E) None of these

Answer 1

When two lines one real axis and the other imaginary axis passes perpendicular through a circle, the circle is divided into four quadrants. Into quadrant I where both x and y-axis are positive, Quadrant II here x-axis is negative, and the y-axis is positive, Quadrant III here both the x-axis and y-axis are negative and in Quadrant IV x-axis is positive, and the y-axis is negative. Let us solve this.

Complete step by step answer:
In case of the trigonometric functions in quadrant I all the functions are positive, in Quadrant II, $\sin$ and $cosec$ functions are positive, and other functions are negative, in Quadrant III; $tan$, and $cot$ functions are positive and other are negative, and in the case of Quadrant IV, $cos$ and $sec$ functions are positive and other being negative.

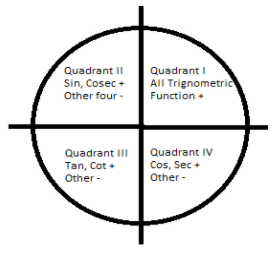
In this question, the value of $\sin {\left( {231} \right)^ \circ }$ is to be found, where ${\left( {231} \right)^ \circ }$ it lies in the third quadrant. So, we need to use trigonometric identities to get the result.
As ${\left( {231} \right)^ \circ }$ lies in between $\left( {{{180}^0},{{270}^0}} \right)$ so, we can say that ${\left( {231} \right)^ \circ }$ lies in the third quadrant.
Using the trigonometric identity of $\sin \left( {\dfrac{{n\pi }}{2} - \theta } \right) = \pm \cos \theta$ , we can rewrite the given trigonometric function $\sin {\left( {231} \right)^ \circ }$ as:

=\pm \cos {39^0} - - - - (i)$$ Moreover, following the above figure, we can say that $\sin \theta $ is negative in third-quadrant. Hence, equation (i) can be written as: $\sin \left( {{{231}^0}} \right) = - \cos {39^0}$ _**Hence the option B is correct.**_ **Note:** Students must be aware of the sign convention of the trigonometric functions in different quadrants. Moreover, it should always be remembered that the angle in trigonometric functions is measured in an anti-clockwise direction only.