Question

The value of $\sin \frac{9\pi}{14} \sin \frac{11\pi}{14} \sin \frac{13\pi}{14}$ is equal to

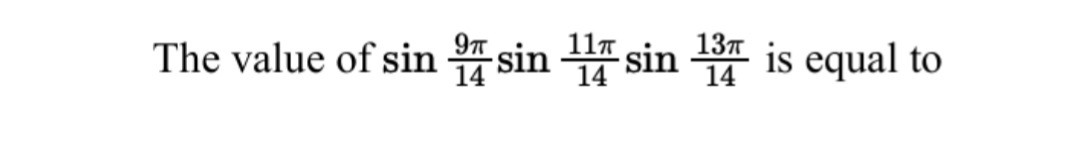
• A. 1/8
• B. -1/8
• C. 1/4
• D. -1/4

Answer 1

Answer: (A)

1/8

Answer 2

Let the given expression be $E$. $E = \sin \frac{9\pi}{14} \sin \frac{11\pi}{14} \sin \frac{13\pi}{14}$ Using $\sin(\pi - x) = \sin x$: $E = \sin \left(\pi - \frac{5\pi}{14}\right) \sin \left(\pi - \frac{3\pi}{14}\right) \sin \left(\pi - \frac{\pi}{14}\right)$ $E = \sin \frac{5\pi}{14} \sin \frac{3\pi}{14} \sin \frac{\pi}{14}$ Using $\sin x = \cos\left(\frac{\pi}{2} - x\right)$: $E = \cos\left(\frac{\pi}{2} - \frac{5\pi}{14}\right) \cos\left(\frac{\pi}{2} - \frac{3\pi}{14}\right) \cos\left(\frac{\pi}{2} - \frac{\pi}{14}\right)$ $E = \cos \frac{2\pi}{14} \cos \frac{4\pi}{14} \cos \frac{6\pi}{14}$ $E = \cos \frac{\pi}{7} \cos \frac{2\pi}{7} \cos \frac{3\pi}{7}$ Multiply and divide by $2 \sin \frac{\pi}{7}$: $E = \frac{2 \sin \frac{\pi}{7} \cos \frac{\pi}{7} \cos \frac{2\pi}{7} \cos \frac{3\pi}{7}}{2 \sin \frac{\pi}{7}}$ $E = \frac{\sin \frac{2\pi}{7} \cos \frac{2\pi}{7} \cos \frac{3\pi}{7}}{2 \sin \frac{\pi}{7}}$ Multiply by 2/2: $E = \frac{2 \sin \frac{2\pi}{7} \cos \frac{2\pi}{7} \cos \frac{3\pi}{7}}{4 \sin \frac{\pi}{7}} = \frac{\sin \frac{4\pi}{7} \cos \frac{3\pi}{7}}{4 \sin \frac{\pi}{7}}$ Using $\sin \frac{4\pi}{7} = \sin (\pi - \frac{3\pi}{7}) = \sin \frac{3\pi}{7}$: $E = \frac{\sin \frac{3\pi}{7} \cos \frac{3\pi}{7}}{4 \sin \frac{\pi}{7}}$ Multiply by 2/2: $E = \frac{2 \sin \frac{3\pi}{7} \cos \frac{3\pi}{7}}{8 \sin \frac{\pi}{7}} = \frac{\sin \frac{6\pi}{7}}{8 \sin \frac{\pi}{7}}$ Using $\sin \frac{6\pi}{7} = \sin (\pi - \frac{\pi}{7}) = \sin \frac{\pi}{7}$: $E = \frac{\sin \frac{\pi}{7}}{8 \sin \frac{\pi}{7}} = \frac{1}{8}$