Solveeit Logo
Login

Question

Question: The value of \({{\sin }^{-1}}\left( \cos \left( {{\cos }^{-1}}\cos x+{{\sin }^{-1}}\sin x \right) \r...

The value of sin⁡−1(cos⁡(cos⁡−1cos⁡x+sin⁡−1sin⁡x)){{\sin }^{-1}}\left( \cos \left( {{\cos }^{-1}}\cos x+{{\sin }^{-1}}\sin x \right) \right), where x∈(π2,π)x\in \left( \dfrac{\pi }{2},\pi \right) is equal to
[a] π2\dfrac{\pi }{2}
[b] π\pi
[c] −π-\pi
[d] −π2-\dfrac{\pi }{2}

Explanation

Solution

Hint: Use the fact that if sin⁡x=sin⁡y,\sin x=\sin y, then x=nπ+(−1)ny,n∈Zx=n\pi +{{\left( -1 \right)}^{n}}y,n\in \mathbb{Z} and sin⁡−1x∈[−π2,π2]{{\sin }^{-1}}x\in \left[ \dfrac{-\pi }{2},\dfrac{\pi }{2} \right] and if cos⁡x=cos⁡y\cos x=\cos y, then x=2nπ±y,n∈Zx=2n\pi \pm y,n\in \mathbb{Z} and cos⁡−1x∈[0,π]{{\cos }^{-1}}x\in \left[ 0,\pi \right]. Assume u=cos⁡−1(cos⁡x)u={{\cos }^{-1}}\left( \cos x \right) and hence prove that u=2nπ±x,n∈Zu=2n\pi \pm x,n\in \mathbb{Z}. Find the suitable value of n such that u∈[0,2π]u\in \left[ 0,2\pi \right]. Hence find the value of u. Similarly, assume v=sin⁡−1(sin⁡x)v={{\sin }^{-1}}\left( \sin x \right) and hence prove that v=nπ+(−1)nx,n∈Zv=n\pi +{{\left( -1 \right)}^{n}}x,n\in \mathbb{Z}. Find the suitable value of n such that v∈[−π2,π2]v\in \left[ \dfrac{-\pi }{2},\dfrac{\pi }{2} \right]. Hence find the value of v. Hence find the value of cos⁡(cos⁡−1cos⁡x+sin⁡−1sin⁡x)\cos \left( {{\cos }^{-1}}\cos x+{{\sin }^{-1}}\sin x \right) and hence evaluate the given expression.

Complete step-by-step answer:
Let u=cos⁡−1cos⁡xu={{\cos }^{-1}}\cos x
We know that if y=cos⁡−1x⇒x=cos⁡yy={{\cos }^{-1}}x\Rightarrow x=\cos y
Hence, we have
cos⁡u=cos⁡x\cos u=\cos x
We know that if cos⁡x=cos⁡y\cos x=\cos y, then x=2nπ±y,n∈Zx=2n\pi \pm y,n\in \mathbb{Z}
Hence, we have
u=2nπ±x,n∈Zu=2n\pi \pm x,n\in \mathbb{Z}
We know that cos⁡−1x∈[0,π]{{\cos }^{-1}}x\in \left[ 0,\pi \right]
Hence, we have u∈[0,π]u\in \left[ 0,\pi \right]
Now since x∈(π2,π)x\in \left( \dfrac{\pi }{2},\pi \right), we have x∈[0,π]x\in \left[ 0,\pi \right]
Hence, we have
u=xu=x
Now, let v=sin⁡−1sin⁡xv={{\sin }^{-1}}\sin x
Hence, we have
sin⁡v=sin⁡x\sin v=\sin x
We know that if sin⁡x=sin⁡y,\sin x=\sin y, then x=nπ+(−1)ny,n∈Zx=n\pi +{{\left( -1 \right)}^{n}}y,n\in \mathbb{Z}
Hence, we have
v=nπ+(−1)nxv=n\pi +{{\left( -1 \right)}^{n}}x
Since sin⁡−1x∈[−π2,π2]{{\sin }^{-1}}x\in \left[ \dfrac{-\pi }{2},\dfrac{\pi }{2} \right], we have
v∈[−π2,π2]v\in \left[ \dfrac{-\pi }{2},\dfrac{\pi }{2} \right]
Now since x∈(π2,π),x\in \left( \dfrac{\pi }{2},\pi \right), we have π−x∈[−π2,π2]\pi -x\in \left[ \dfrac{-\pi }{2},\dfrac{\pi }{2} \right]
Hence, we have
v=π−xv=\pi -x
Hence, we have
sin⁡−1sin⁡x+cos⁡−1cos⁡x=v+u=π−x+x=π{{\sin }^{-1}}\sin x+{{\cos }^{-1}}\cos x=v+u=\pi -x+x=\pi
Hence, we have
cos⁡(sin⁡−1sin⁡x+cos⁡−1cos⁡x)=cos⁡π=−1\cos \left( {{\sin }^{-1}}\sin x+{{\cos }^{-1}}\cos x \right)=\cos \pi =-1
We know that sin⁡−1(−x)=−sin⁡−1x{{\sin }^{-1}}\left( -x \right)=-{{\sin }^{-1}}x
Hence, we have
sin⁡(cos⁡(sin⁡−1sin⁡x+cos⁡−1cos⁡x))=sin⁡−1(−1)=−sin⁡−11\sin \left( \cos \left( {{\sin }^{-1}}\sin x+{{\cos }^{-1}}\cos x \right) \right)={{\sin }^{-1}}\left( -1 \right)=-{{\sin }^{-1}}1
We know that sin⁡−1(1)=π2{{\sin }^{-1}}\left( 1 \right)=\dfrac{\pi }{2}
Hence, we have
sin⁡(cos⁡(sin⁡−1sin⁡x+cos⁡−1cos⁡x))=−π2\sin \left( \cos \left( {{\sin }^{-1}}\sin x+{{\cos }^{-1}}\cos x \right) \right)=-\dfrac{\pi }{2}
Hence option [d] is correct.

Note: Alternative solution:
We know that
{{\sin }^{-1}}\sin \left( x \right)=\left\\{ \begin{matrix} \vdots \\\ -\pi -x,x\in \left[ \dfrac{-3\pi }{2},\dfrac{-\pi }{2} \right] \\\ x,x\in \left[ \dfrac{-\pi }{2},\dfrac{\pi }{2} \right] \\\ \pi -x,x\in \left[ \dfrac{\pi }{2},\dfrac{3\pi }{2} \right] \\\ \vdots \\\ \end{matrix} \right. and {{\cos }^{-1}}\cos x=\left\\{ \begin{matrix} \vdots \\\ 2\pi +x,x\in \left[ -2\pi ,-\pi \right] \\\ x,x\in \left[ 0,\pi \right] \\\ 2\pi -x,x\in \left[ \pi ,2\pi \right] \\\ \vdots \\\ \end{matrix} \right.
Using these definitions, we can find the value of the above expression.
Graph of sin⁡−1sin⁡x{{\sin }^{-1}}\sin x:

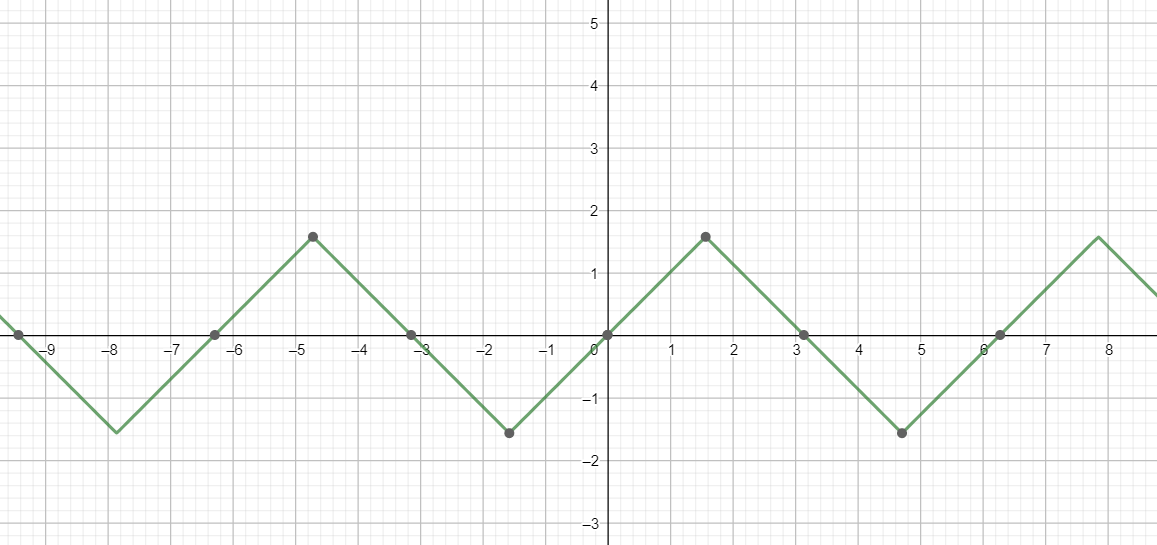
Graph of cos⁡−1cos⁡x{{\cos }^{-1}}\cos x: