Question
Question: The value of resistance $R$ is being measured with the potentiometer set up in two steps shown below...
The value of resistance R is being measured with the potentiometer set up in two steps shown below. Step-I : Es=10 V, r=1Ω and zero deflection is observed at length PJ=80 cm. Step-II : Es=5 V, r=2Ω and zero deflection is observed at length PJ=30 cm. Then
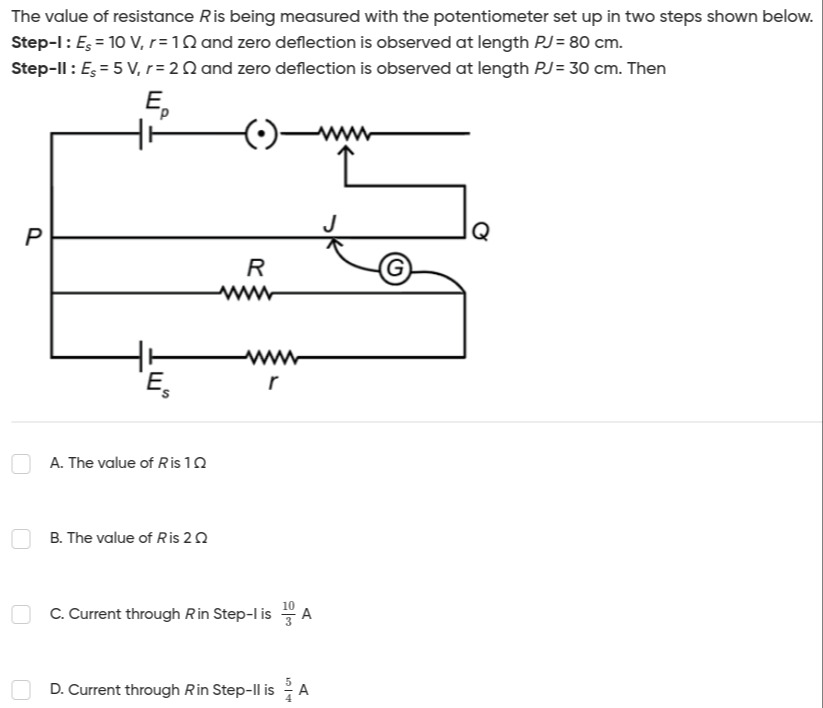
The value of R is 1Ω
The value of R is 2Ω
Current through R in Step-I is 310A
Current through R in Step-II is 45A
The value of R is 2Ω, Current through R in Step-I is 310A, Current through R in Step-II is 45A
Solution
The problem involves a potentiometer circuit used to determine an unknown resistance R. The principle of a potentiometer states that at null deflection, the potential difference across the balancing length of the potentiometer wire is equal to the potential difference across the component in the secondary circuit.
The secondary circuit consists of a cell Es, an internal resistance r, and the unknown resistance R. The current flowing through this secondary circuit is given by Ohm's law: Is=R+rEs
The potential difference across the unknown resistance R is: VR=Is×R=R+rEsR
At null deflection, this potential difference VR is balanced by the potential drop across the balancing length L of the potentiometer wire. If k is the potential gradient of the potentiometer wire (potential drop per unit length), then: k×L=VR So, k×L=R+rEsR
We are given two steps:
Step-I: Es=10 V r=1Ω L=80 cm Substituting these values into the equation: k×80=R+110×R (Equation 1)
Step-II: Es=5 V r=2Ω L=30 cm Substituting these values into the equation: k×30=R+25×R (Equation 2)
To find R, we can divide Equation 1 by Equation 2: k×30k×80=R+25RR+110R 38=R+110R×5RR+2 The R in the numerator and denominator on the right side cancels out, and 10/5=2: 38=R+12(R+2) Now, cross-multiply: 8(R+1)=3×2(R+2) 8R+8=6R+12 8R−6R=12−8 2R=4 R=2Ω
So, option B is correct.
Now, let's calculate the currents through R for both steps:
Current through R in Step-I (Is1): Is1=R+rEs=2Ω+1Ω10 V=310 A So, option C is correct.
Current through R in Step-II (Is2): Is2=R+rEs=2Ω+2Ω5 V=45 A So, option D is correct.
Option A states R=1Ω, which is incorrect.
Thus, options B, C, and D are all correct.
