Question

The value of \mathop \smallint \nolimits_{ - 2}^2 \begin{array}{*{20}{c}} {\min \left\\{ {x - \left[ x \right], - x - \left[ { - x} \right]} \right\\}} \\\ \; \end{array} is equal to ….?

Answer 1

The relation between number ‘x’, integral part of x, ‘[x]’; and fractional part of x, ‘{x}’ is given by
$x = [x] + \\{ x\\}$
Any function which is in the form of min(x,y) takes a minimum value from x and y in a given interval.

Complete step by step solution:
Step 1: - Here is the first step,
x = \left[ x \right] + \left\\{ x \right\\}
\left\\{ x \right\\} = \;x - \left[ x \right]
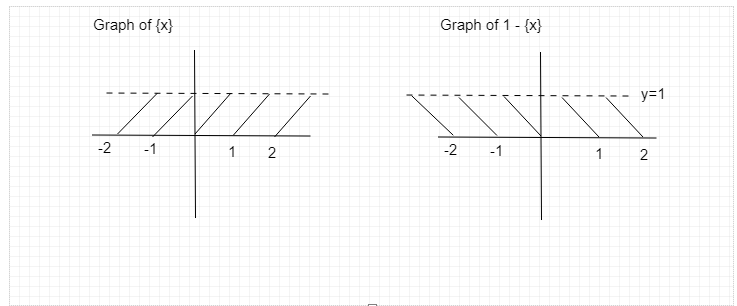
x - \left[ x \right] = \left\\{ x \right\\} …………….(i)
Similarly:
$- x - \left[ { - x} \right] = \left( { - x} \right) - \left[ {\left( { - x} \right)} \right]$
= \left\\{ { - x} \right\\}
= 1 - \left\\{ x \right\\} \ldots \ldots \ldots \ldots \ldots \ldots ..\left( {ii} \right)

Step 2: - In next step, We will use the graph for draw the graphical representation of (1) and (2)

Step 3: - So, In third step, We need to Combined graphical representation of (1) and (2)

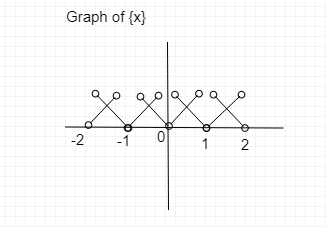
Step 4: In the last step, Here we need to find the minimum bounded region
Now $\int_{ - 2}^2 {min\\{ x - [x], - x - [x]} \\}$ $= 4 \times Area\;of\;\Delta ABC$
$= 4 \times \dfrac{1}{2} \times base \times height$
$= 4 \times \dfrac{1}{2} \times 1 \times \dfrac{1}{2}$
$= \;4 \times \dfrac{1}{4}$
$= 1$
$\int\limits_{ - 2}^2 {min\\{ x - [x], - x - [x]\\} = 1}$
Note:
Geometrical representation of a definite integral. Let f be a continuous function on [a, b] and f(x) >= 0 x belongs to [a, b], then \mathop \smallint \nolimits_a^b f\left( x \right)\;dx represents the area of the region bounded on the left by the line x = a on the right by x = b below by x – axis and above the curve y = f(x)

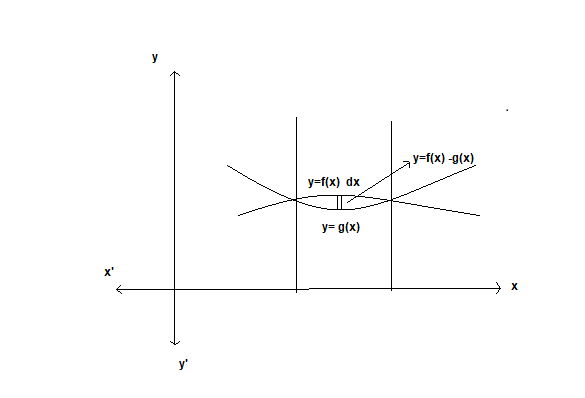
Given curves represented by y= f(x), y-= g(x) where f(x) >= g(x) in [a, b]

Elementary strip has height f(x) – g(x) and width dx so that the elementary area = [f(x) – g(x)dx, and total area takes an A = ∴ \mathop \smallint \nolimits_a^b [{\text{f}}\left( x \right) - g\left( x \right)]dx