Solveeit Logo
Login

Question

Question: The value of $\log_{10}\left(\frac{\sum\limits_{i=0}^{r}{^{n}C_{2i}\ ^{n-2i}C_{r-i}}}{\sum\limits_{i...

The value of log⁡10(∑i=0rnC2i n−2iCr−i∑i=rnnCi 2iC2r(34)n−i(14)i−r)\log_{10}\left(\frac{\sum\limits_{i=0}^{r}{^{n}C_{2i}\ ^{n-2i}C_{r-i}}}{\sum\limits_{i=r}^{n}{^{n}C_{i}\ ^{2i}C_{2r}\left(\frac{3}{4}\right)^{n-i}\left(\frac{1}{4}\right)^{i-r}}}\right) (n≥2r)(n \ge 2r) is :

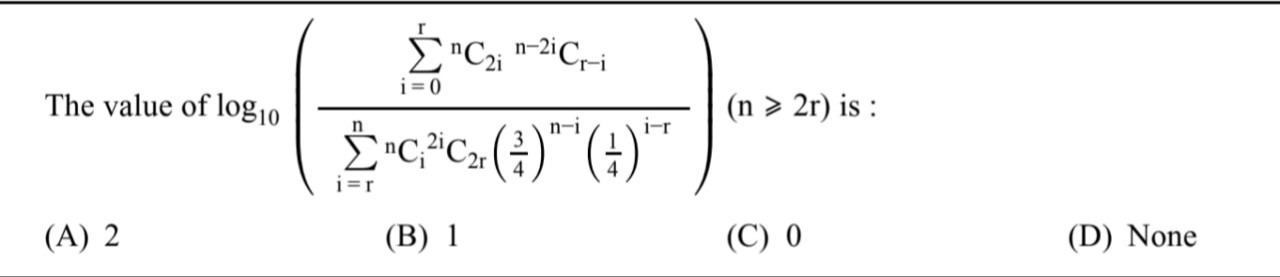
A

2

B

1

C

0

D

None

Answer

0

Explanation

Solution

We wish to evaluate

L=log⁡10(ND),whereN=∑i=0r(n2i)(n−2ir−i),L=\log_{10}\left(\frac{N}{D}\right),\quad\text{where}\quad N=\sum_{i=0}^{r} \binom{n}{2i}\binom{n-2i}{r-i}, D=∑i=rn(ni)(2i2r)(34)n−i(14) i−r,D=\sum_{i=r}^{n} \binom{n}{i}\binom{2i}{2r}\left(\frac{3}{4}\right)^{n-i}\left(\frac{1}{4}\right)^{\,i-r},

with n≥2rn\ge 2r.

A good strategy is to “test” the expression for small values of nn and rr and see if a pattern emerges.

Step 1. Testing for r=1,  n=2r=1,\; n=2:

The numerator:

N=(20)(21)+(22)(00)=(1⋅2)+(1⋅1)=2+1=3.N=\binom{2}{0}\binom{2}{1}+\binom{2}{2}\binom{0}{0} = (1\cdot2)+(1\cdot1) = 2+1 = 3.

The denominator:

D=(21)(22)(34)1(14)0+  (22)(42)(34)0(14)1=2⋅1⋅34+1⋅6⋅1⋅14=64+64=124=3.\begin{array}{rcl} D &=& \binom{2}{1}\binom{2}{2}\left(\frac{3}{4}\right)^{1}\left(\frac{1}{4}\right)^{0} \\ && +\;\binom{2}{2}\binom{4}{2}\left(\frac{3}{4}\right)^{0}\left(\frac{1}{4}\right)^{1} \\ &=& 2\cdot 1 \cdot \frac{3}{4} + 1\cdot 6 \cdot 1 \cdot \frac{1}{4} \\ &=& \frac{6}{4}+\frac{6}{4}=\frac{12}{4}=3. \end{array}

Thus, ND=33=1\frac{N}{D}= \frac{3}{3}=1 so that

L=log⁡10(1)=0.L=\log_{10}(1)=0.

Step 2. Testing for r=1,  n=3r=1,\; n=3:

The numerator:

N=(30)(31)+(32)(10)=1⋅3+3⋅1=3+3=6.N=\binom{3}{0}\binom{3}{1}+\binom{3}{2}\binom{1}{0} = 1\cdot3+3\cdot1=3+3=6.

The denominator:

D=(31)(22)(34)2(14)0+ (32)(42)(34)1(14)1+ (33)(62)(34)0(14)2=3⋅1⋅916+3⋅6⋅34⋅14+1⋅15⋅1⋅116=2716+5416+1516=9616=6.\begin{array}{rcl} D &=& \binom{3}{1}\binom{2}{2}\left(\frac{3}{4}\right)^{2}\left(\frac{1}{4}\right)^{0} \\ &&+\,\binom{3}{2}\binom{4}{2}\left(\frac{3}{4}\right)^{1}\left(\frac{1}{4}\right)^{1} \\ &&+\,\binom{3}{3}\binom{6}{2}\left(\frac{3}{4}\right)^{0}\left(\frac{1}{4}\right)^{2} \\ &=& 3\cdot 1 \cdot \frac{9}{16}+3\cdot 6 \cdot \frac{3}{4}\cdot\frac{1}{4}+1\cdot15\cdot 1\cdot\frac{1}{16} \\ &=& \frac{27}{16}+\frac{54}{16}+\frac{15}{16}=\frac{96}{16}=6. \end{array}

Thus, ND=6/6=1\frac{N}{D}=6/6=1 and again

L=log⁡10(1)=0.L=\log_{10}(1)=0.

Step 3. Testing for r=2,  n=5r=2,\; n=5:

The numerator:

N=(50)(52)+(52)(31)+(54)(10)=1⋅10+10⋅3+5⋅1=10+30+5=45.\begin{array}{rcl} N &=& \binom{5}{0}\binom{5}{2}+\binom{5}{2}\binom{3}{1}+\binom{5}{4}\binom{1}{0} \\ &=& 1\cdot10+10\cdot3+5\cdot1 \\ &=& 10+30+5=45. \end{array}

Now, the denominator:

D=(52)(44)(34)3(14)0+ (53)(64)(34)2(14)1+ (54)(84)(34)1(14)2+ (55)(104)(34)0(14)3=10⋅1⋅2764+10⋅15⋅916⋅14+ 5⋅70⋅34⋅116+1⋅210⋅1⋅164=27064+135064+105064+21064=270+1350+1050+21064=288064=45.\begin{array}{rcl} D &=& \binom{5}{2}\binom{4}{4}\left(\frac{3}{4}\right)^{3}\left(\frac{1}{4}\right)^{0} \\ &&+\,\binom{5}{3}\binom{6}{4}\left(\frac{3}{4}\right)^{2}\left(\frac{1}{4}\right)^{1} \\ &&+\,\binom{5}{4}\binom{8}{4}\left(\frac{3}{4}\right)^{1}\left(\frac{1}{4}\right)^{2} \\ &&+\,\binom{5}{5}\binom{10}{4}\left(\frac{3}{4}\right)^{0}\left(\frac{1}{4}\right)^{3}\\[1mm] &=& 10\cdot1\cdot\frac{27}{64}+10\cdot15\cdot\frac{9}{16}\cdot\frac{1}{4}\\[1mm] &&+\,5\cdot70\cdot\frac{3}{4}\cdot\frac{1}{16}+1\cdot210\cdot 1\cdot\frac{1}{64}\\[1mm] &=& \frac{270}{64}+\frac{1350}{64}+\frac{1050}{64}+\frac{210}{64}\\[1mm] &=& \frac{270+1350+1050+210}{64}=\frac{2880}{64}=45. \end{array}

Again, ND=45/45=1\frac{N}{D} =45/45=1 so that

L=log⁡10(1)=0.L=\log_{10}(1)=0.

Since the ratio ND\frac{N}{D} consistently equals 1, we conclude that

log⁡10(ND)=log⁡10(1)=0.\log_{10}\left(\frac{N}{D}\right)=\log_{10}(1)=0.

Thus, the answer is 0\mathbf{0} corresponding to option (C).