Question

The value of $\lim_{x\to 0} \left(\frac{\int_{0}^{x^2}sec^2t \ dt}{xsinx}\right)$ is

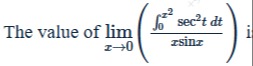
Answer 1

1

Answer 2

The limit is of the form $\frac{0}{0}$. Using L'Hôpital's Rule twice or using the integral $\int sec^2 t dt = \tan t$ and standard limits, we find the value of the limit.

Using the integral result, the expression becomes $\frac{\tan(x^2)}{x\sin x}$.

Rewrite as $\frac{\tan(x^2)}{x^2} \cdot \frac{x}{\sin x}$.

Using standard limits $\lim_{u\to 0} \frac{\tan u}{u} = 1$ and $\lim_{x\to 0} \frac{x}{\sin x} = 1$, the limit evaluates to $1 \times 1 = 1$.