Question

The value of $\lim_{x \to 0} \frac{(2^{\sin x}-1).\ln(1+\sin2x)}{x(\tan^{-1}x)}$ is $\ln k$. The value of k is _______.

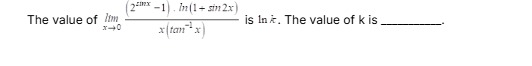
Answer 1

4

Answer 2

We are asked to find the value of $k$ where the given limit is equal to $\ln k$.

The limit is: $L = \lim_{x \to 0} \frac{(2^{\sin x}-1) \cdot \ln(1+\sin2x)}{x \cdot \tan^{-1}x}$

We can rewrite the expression by multiplying and dividing by appropriate terms to utilize standard limits: $L = \lim_{x \to 0} \left( \frac{2^{\sin x}-1}{\sin x} \cdot \frac{\ln(1+\sin2x)}{\sin2x} \cdot \frac{\sin x}{x} \cdot \frac{\sin2x}{x} \cdot \frac{x}{\tan^{-1}x} \right)$

Now, we evaluate each part using standard limits:

1. $\lim_{x \to 0} \frac{2^{\sin x}-1}{\sin x}$: Let $u = \sin x$. As $x \to 0$, $u \to 0$. This becomes $\lim_{u \to 0} \frac{2^u-1}{u} = \ln 2$.
2. $\lim_{x \to 0} \frac{\ln(1+\sin2x)}{\sin2x}$: Let $v = \sin 2x$. As $x \to 0$, $v \to 0$. This becomes $\lim_{v \to 0} \frac{\ln(1+v)}{v} = 1$.
3. $\lim_{x \to 0} \frac{\sin x}{x} = 1$.
4. $\lim_{x \to 0} \frac{\sin2x}{x} = \lim_{x \to 0} \frac{\sin2x}{2x} \cdot 2 = 1 \cdot 2 = 2$.
5. $\lim_{x \to 0} \frac{x}{\tan^{-1}x} = \frac{1}{\lim_{x \to 0} \frac{\tan^{-1}x}{x}} = \frac{1}{1} = 1$.

Multiplying these limits together: $L = (\ln 2) \cdot (1) \cdot (1) \cdot (2) \cdot (1) = 2 \ln 2$

We are given that the limit is equal to $\ln k$: $2 \ln 2 = \ln k$

Using the logarithm property $m \ln a = \ln a^m$: $\ln (2^2) = \ln k$ $\ln 4 = \ln k$

Therefore, $k = 4$.