Question
Question: The value of $\left(\frac{\sin \frac{2\pi}{9}-i \cos \frac{2\pi}{9}}{\cos \frac{2\pi}{3}+i \sin \fra...
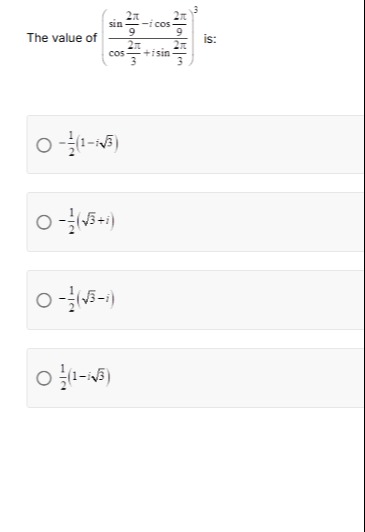
The value of (cos32π+isin32πsin92π−icos92π)3 is:
A
−21(1−i3)
B
−21(3+i)
C
−21(3−i)
D
21(1−i3)
Answer
−21(3+i)
Explanation
Solution
To solve this, we express the numerator and denominator in exponential form:
sin92π−icos92π=ei(92π−2π),cos32π+isin32π=ei32π
Then, compute the division, take the power of 3, reduce modulo 2π, and convert to rectangular form.
