Question
Question: The value of $\int_{0}^{[x]} \frac{2^x}{2^{[x]}}dx$ is...
The value of ∫0[x]2[x]2xdx is
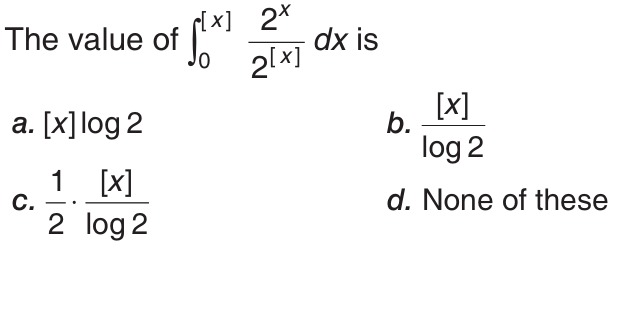
[x]log2
log2[x]
21⋅log2[x]
None of these
log2[x]
Solution
Let the given integral be I. The upper limit of the integral is [x]. Let n=[x]. Since the lower limit is 0, we consider the case where n is a non-negative integer. If x≥0, then [x]≥0. The integral is I=∫0n2[x]2xdx.
We can split the integral into a sum of integrals over the intervals [k,k+1) for k=0,1,…,n−1. In each interval [k,k+1), the value of [x] is k. So, we can write the integral as: I=∑k=0n−1∫kk+12[x]2xdx
For x∈[k,k+1), [x]=k. Thus, the integrand becomes 2k2x. The integral over the interval [k,k+1) is: ∫kk+12k2xdx=2k1∫kk+12xdx
Now, we evaluate the integral ∫2xdx. The formula for the integral of ax is ∫axdx=logaax+C. So, ∫2xdx=log22x+C.
Now, evaluate the definite integral ∫kk+12xdx: ∫kk+12xdx=[log22x]kk+1=log22k+1−log22k=log22k+1−2k =log22⋅2k−2k=log22k(2−1)=log22k
Substitute this result back into the integral over the interval [k,k+1): ∫kk+12k2xdx=2k1⋅log22k=log21
The total integral is the sum of these integrals over the intervals from k=0 to n−1. There are n such intervals. I=∑k=0n−1log21
This is a sum of n terms, each equal to log21. I=n⋅log21=log2n
Since n=[x], the value of the integral is log2[x].
