Question

The value of $\int_{0}^{\sqrt{2}}[x^2]dx$, where [:] is the greatest integer function, is

Answer 1

$\sqrt{2} - 1$

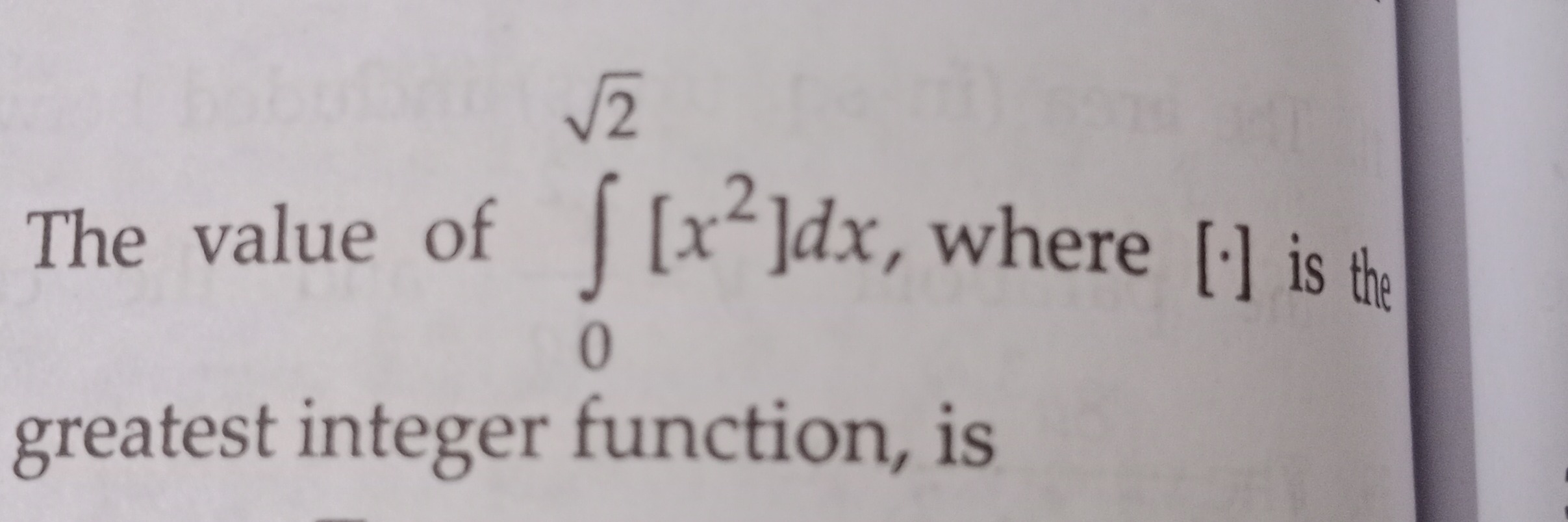
Answer 2

1. Interval Analysis:

   • For $x \in [0,1)$: $x^2 \in [0,1)$ and hence $[x^2] = 0$.
   • For $x \in [1,\sqrt{2}]$: $x^2 \in [1,2]$ and hence $[x^2] = 1$ (the endpoint $x = \sqrt{2}$ doesn't affect the integral since it has measure zero).

2. Splitting the Integral:

   $$\int_{0}^{\sqrt{2}} [x^2]\,dx = \int_{0}^{1} 0\,dx + \int_{1}^{\sqrt{2}} 1\,dx$$ $$= 0 + (\sqrt{2} - 1) = \sqrt{2} - 1.$$

Explanation (Minimal):

• Interval $[0,1)$: floor is 0.
• Interval $[1,\sqrt{2}]$: floor is 1.
• Thus, the integral evaluates to $\sqrt{2} - 1$.