Question
Question: The value of $\int_{0}^{1}\frac{ln(x+x^{-1})}{x+x^{-1}}dx$ equals (It is given that $\sum_{n=1}^{\in...
The value of ∫01x+x−1ln(x+x−1)dx equals (It is given that ∑n=1∞n2(−1)n+1=12π2)
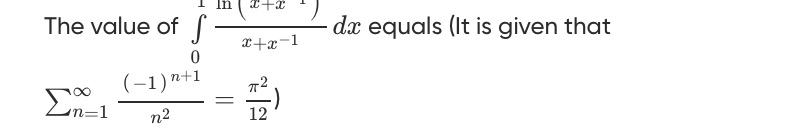
4(ln2)2−48π2
Solution
The given integral is I=∫01x+x−1ln(x+x−1)dx.
First, simplify the term x+x−1=x+x1=xx2+1. So the integral becomes I=∫01xx2+1ln(xx2+1)dx.
Let's use the substitution x=tanθ. When x=0, θ=0. When x=1, θ=4π. dx=sec2θdθ. The term x+x−1 becomes tanθ+tanθ1=cosθsinθ+sinθcosθ=sinθcosθsin2θ+cos2θ=sinθcosθ1=2sinθcosθ2=sin(2θ)2.
Substitute these into the integral: I=∫0π/4sin(2θ)2ln(sin(2θ)2)sec2θdθ I=∫0π/42sin(2θ)ln(sin(2θ)2)sec2θdθ Using sin(2θ)=2sinθcosθ and sec2θ=cos2θ1: I=∫0π/422sinθcosθ(ln2−ln(sin(2θ)))cos2θ1dθ I=∫0π/4cosθsinθ(ln2−ln(sin(2θ)))dθ I=∫0π/4tanθ(ln2−ln(sin(2θ)))dθ Split the integral into two parts: I=ln2∫0π/4tanθdθ−∫0π/4tanθln(sin(2θ))dθ
Evaluate the first integral: ∫0π/4tanθdθ=[ln∣secθ∣]0π/4=ln(sec(π/4))−ln(sec(0))=ln(2)−ln(1)=21ln2−0=21ln2 So the first term is ln2⋅21ln2=21(ln2)2.
Now, let J=∫0π/4tanθln(sin(2θ))dθ. Apply integration by parts: ∫udv=uv−∫vdu. Let u=ln(sin(2θ)) and dv=tanθdθ. Then du=sin(2θ)1⋅2cos(2θ)dθ=2cot(2θ)dθ. And v=∫tanθdθ=ln∣secθ∣.
J=[ln∣secθ∣ln(sin(2θ))]0π/4−∫0π/4ln∣secθ∣⋅2cot(2θ)dθ Evaluate the boundary term: At θ=4π: ln(sec(π/4))ln(sin(π/2))=ln(2)ln(1)=21ln2⋅0=0. At θ=0: limθ→0+ln(secθ)ln(sin(2θ)). This is a 0×(−∞) form. Using L'Hopital's rule or series expansion: ln(secθ)=−ln(cosθ)≈−(2θ2−1)≈2θ2 for small θ. ln(sin(2θ))≈ln(2θ) for small θ. So the limit is limθ→0+2θ2ln(2θ). Let y=2θ. limy→0+8y2lny=0. Thus, the boundary term is 0.
So, J=−∫0π/4ln∣secθ∣⋅2cot(2θ)dθ=∫0π/4ln(cosθ)⋅2cot(2θ)dθ. We have 2cot(2θ)=sin(2θ)2cos(2θ)=2sinθcosθ2(2cos2θ−1)=sinθcosθ2cos2θ−1=sinθ2cosθ−sinθcosθ1=2cotθ−2csc(2θ). So, J=∫0π/4ln(cosθ)(2cotθ−2csc(2θ))dθ. This approach seems to lead to more complex integrals.
Let's use a different substitution in the original integral. I=∫01x+x−1ln(x+x−1)dx. Let u=x+x1. Then du=(1−x21)dx=x2x2−1dx. This doesn't seem to simplify the integral directly.
Consider the property of definite integrals: ∫abf(x)dx=∫abf(a+b−x)dx. Here a=0,b=1. So x→1−x. I=∫01(1−x)+(1−x)−1ln((1−x)+(1−x)−1)dx. This makes it more complicated.
Let's try a substitution x=e−t. When x=0, t→∞. When x=1, t=0. dx=−e−tdt. x+x−1=e−t+et=2cosht. I=∫∞02coshtln(2cosht)(−e−t)dt I=∫0∞2coshtln(2cosht)e−tdt Expand 2cosht=et+e−t: I=∫0∞et+e−tln(et+e−t)e−tdt I=∫0∞et(1+e−2t)ln(et(1+e−2t))e−tdt I=∫0∞et+e−tt+ln(1+e−2t)e−tdt I=∫0∞et+e−tte−tdt+∫0∞et+e−tln(1+e−2t)e−tdt Multiply numerator and denominator by e−t: I=∫0∞1+e−2tte−2tdt+∫0∞1+e−2tln(1+e−2t)e−2tdt Let u=e−2t. Then du=−2e−2tdt. So e−2tdt=−21du. Also, t=−21lnu. When t=0, u=e0=1. When t=∞, u=e−∞=0.
Substitute these into the first integral: I1=∫101+u−21lnu(−21du)=41∫011+ulnudu This is a standard integral. We know that 1+u1=∑n=0∞(−1)nun for ∣u∣<1. So, ∫011+ulnudu=∫01lnu∑n=0∞(−1)nundu=∑n=0∞(−1)n∫01unlnudu. The integral ∫01unlnudu can be evaluated by integration by parts: ∫unlnudu=n+1un+1lnu−∫n+1un+1u1du=n+1un+1lnu−(n+1)2un+1. Evaluating from 0 to 1: [n+1un+1lnu−(n+1)2un+1]01=(0−(n+1)21)−(0−0)=−(n+1)21. (The limit limu→0+un+1lnu=0 for n+1>0.) So, ∫011+ulnudu=∑n=0∞(−1)n(−(n+1)21)=−∑n=0∞(n+1)2(−1)n. Let k=n+1. Then n=k−1. When n=0,k=1. When n=∞,k=∞. So, −∑k=1∞k2(−1)k−1=−∑k=1∞k2−(−1)k=∑k=1∞k2(−1)k. This is related to the given sum ∑n=1∞n2(−1)n+1=12π2. Note that ∑k=1∞k2(−1)k+1=12π2. Our sum is ∑k=1∞k2(−1)k=−∑k=1∞k2(−1)k+1=−12π2. Therefore, I1=41(−12π2)=−48π2.
Now, substitute u=e−2t into the second integral: I2=∫101+uln(1+u)(−21du)=21∫011+uln(1+u)du This integral is of the form ∫ylnydy=2(lny)2. Let y=1+u. Then dy=du. When u=0,y=1. When u=1,y=2. I2=21∫12ylnydy=21[2(lny)2]12 I2=41[(ln2)2−(ln1)2]=41[(ln2)2−0]=4(ln2)2
Finally, I=I1+I2=−48π2+4(ln2)2.
