Question
Question: The value of $\int_{-\frac{\pi}{4}}^{\frac{\pi}{4}} \frac{(\pi-4\theta) \tan \theta}{1-\tan \theta} ...
The value of ∫−4π4π1−tanθ(π−4θ)tanθdθ is equal to:
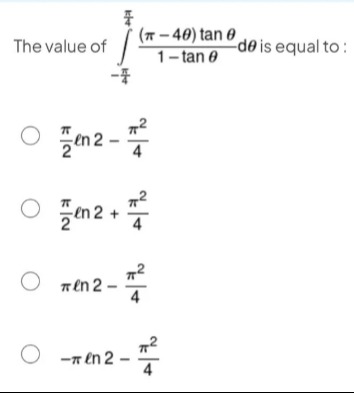
2πln2−4π2
2πln2+4π2
πln2−4π2
−πln2−4π2
πln2−4π2
Solution
We start with
I=∫−4π4π1−tanθ(π−4θ)tanθdθ.A very clever change of variable is to use
u=4π−θ.Then when θ=−4π we have
u=4π−(−4π)=2π,and when θ=4π we get u=0. Also, dθ=−du.
Now, express the integrand in terms of u. Note that
π−4θ=π−4(4π−u)=π−(π−4u)=4u.Next, using the identity
tan(4π−u)=1+tanu1−tanu,we have
1−tan(4π−u)=1−1+tanu1−tanu=1+tanu(1+tanu)−(1−tanu)=1+tanu2tanu.Thus the integrand becomes
1−tanθ(π−4θ)tanθ→1−tan(4π−u)4utan(4π−u)=1+tanu2tanu4u1+tanu1−tanu=2tanu4u(1−tanu)=tanu2u(1−tanu).Changing the limits (and noting that the minus sign from dθ=−du reverses the limits) we write
I=∫u=π/20tanu2u(1−tanu)(−du)=∫0π/2tanu2u(1−tanu)du.It is convenient to rewrite this expression as
I=2∫0π/2u(tanu1−1)du=2∫0π/2u(cotu−1)du.We now separate the integral:
I=2[L∫0π/2ucotudu−M∫0π/2udu].Step 1. Evaluation of M:
M=∫0π/2udu=2u20π/2=8π2.Step 2. Evaluation of L:
Use integration by parts. Let
v=u,dw=cotudu⟹dv=du,w=∫cotudu=ln∣sinu∣.Then
L=uln∣sinu∣0π/2−∫0π/2ln∣sinu∣du.At u=π/2, ln(sin(π/2))=ln1=0; at u=0 the term uln∣sinu∣ tends to 0 (since ulnu→0 as u→0). Hence,
L=−∫0π/2ln(sinu)du.A standard result is:
∫0π/2ln(sinu)du=−2πln2.Thus,
L=−(−2πln2)=2πln2.Step 3. Final answer:
Plug L and M back into the expression for I:
I=2[2πln2−8π2]=πln2−4π2.Summary:
- Explanation: Substitute u=4π−θ, simplify using tan(4π−u)=1+tanu1−tanu to recast the integral as 2∫0π/2u(cotu−1)du. Separate the integral and use integration by parts with the standard formula ∫0π/2ln(sinu)du=−2πln2.
- Answer: πln2−4π2 (Option 3)
