Question

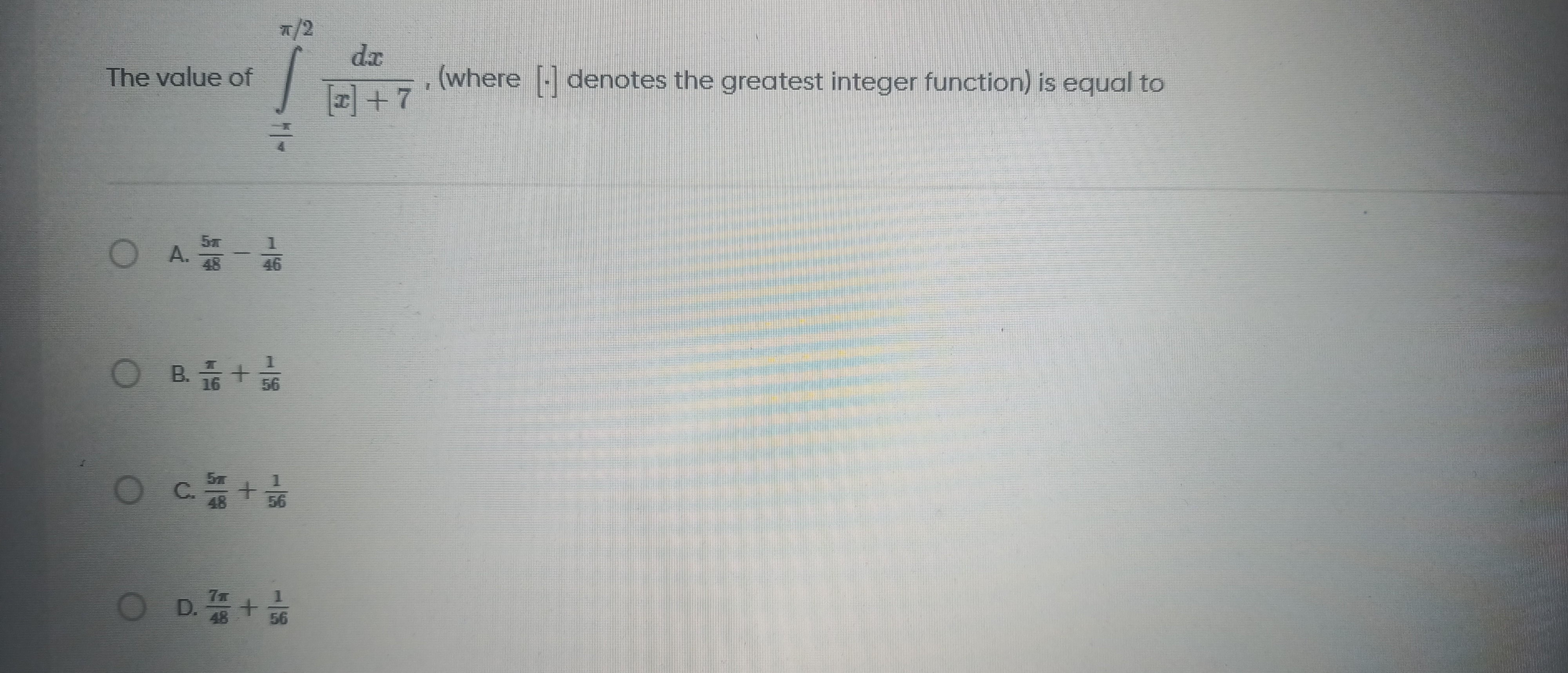
The value of $\int_{-\frac{\pi}{4}}^{\frac{\pi}{2}} \frac{dx}{[x]+7}$, (where [.] denotes the greatest integer function) is equal to

• A. $\frac{5\pi}{48} - \frac{1}{46}$
• B. $\frac{\pi}{16} + \frac{1}{56}$
• C. $\frac{5\pi}{48} + \frac{1}{56}$
• D. $\frac{7\pi}{48} + \frac{1}{56}$

Answer 1

Answer: (C)

$\frac{5\pi}{48} + \frac{1}{56}$

Answer 2

The integral is $\int_{-\frac{\pi}{4}}^{\frac{\pi}{2}} \frac{dx}{[x]+7}$. The limits are approximately $-0.785$ to $1.57$. The greatest integer function $[x]$ changes its value at integer points. In the interval $[-\frac{\pi}{4}, \frac{\pi}{2}]$, the integer points are $0$ and $1$.

We split the integral into three parts:

1. For $x \in [-\frac{\pi}{4}, 0)$, $[x] = -1$.
2. For $x \in [0, 1)$, $[x] = 0$.
3. For $x \in [1, \frac{\pi}{2}]$, $[x] = 1$.

The integral becomes: $\int_{-\frac{\pi}{4}}^{0} \frac{dx}{-1+7} + \int_{0}^{1} \frac{dx}{0+7} + \int_{1}^{\frac{\pi}{2}} \frac{dx}{1+7}$ $= \int_{-\frac{\pi}{4}}^{0} \frac{dx}{6} + \int_{0}^{1} \frac{dx}{7} + \int_{1}^{\frac{\pi}{2}} \frac{dx}{8}$

Evaluating each integral: $\frac{1}{6} [x]_{-\frac{\pi}{4}}^{0} = \frac{1}{6} (0 - (-\frac{\pi}{4})) = \frac{\pi}{24}$ $\frac{1}{7} [x]_{0}^{1} = \frac{1}{7} (1 - 0) = \frac{1}{7}$ $\frac{1}{8} [x]_{1}^{\frac{\pi}{2}} = \frac{1}{8} (\frac{\pi}{2} - 1) = \frac{\pi}{16} - \frac{1}{8}$

Summing these values: $\frac{\pi}{24} + \frac{1}{7} + \frac{\pi}{16} - \frac{1}{8}$ Combine terms with $\pi$: $\frac{\pi}{24} + \frac{\pi}{16} = \pi (\frac{2}{48} + \frac{3}{48}) = \frac{5\pi}{48}$ Combine constant terms: $\frac{1}{7} - \frac{1}{8} = \frac{8}{56} - \frac{7}{56} = \frac{1}{56}$

The total value of the integral is $\frac{5\pi}{48} + \frac{1}{56}$.