Solveeit Logo
Login

Question

Question: The value of \(\int\limits_\pi ^{2\pi } {[2\sin x]dx} \) is equal to (where[.] is the G.I.F.) A. \...

The value of ∫π2π[2sin⁡x]dx\int\limits_\pi ^{2\pi } {[2\sin x]dx} is equal to (where[.] is the G.I.F.)
A. −π- \pi
B. −2π- 2\pi
C. −5π3 - \dfrac{{5\pi }}{3}
D. 5π3\dfrac{{5\pi }}{3}

Explanation

Solution

Greatest Integer Function (G.I.F.) or floor function is a function that rounds off the real number(input) to the greatest integer less than or equal to the number. So here as well, we will first divide the interval over integrand to sub-intervals and then we will check the greatest integer of that interval using the graph of 2sinx i.e., over∫π2π[2sin⁡x]dx\int\limits_\pi ^{2\pi } {[2\sin x]dx} .

Complete step-by-step answer:

Here we are given that we need to find the integral of ∫π2π[2sin⁡x]dx\int\limits_\pi ^{2\pi } {[2\sin x]dx} where [.] is the greatest integer function. So for this, first we will see the graph of the above-mentioned function.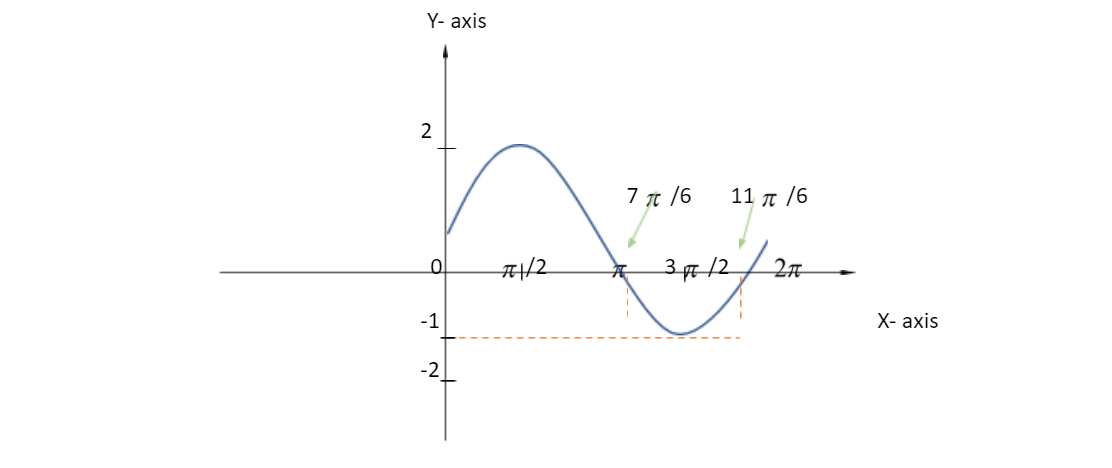

The graph on the right is the graph of 2sinx. We will consider the portion πto2π\pi to2\pi as it is the limit of our given integral.
Here, we can see that we have divided the graph in to intervals(π,7π6),(7π6,3π2),(3π2,11π6),(11π6,2π)\left( {\pi ,\dfrac{{7\pi }}{6}} \right),\left( {\dfrac{{7\pi }}{6},\dfrac{{3\pi }}{2}} \right),\left( {\dfrac{{3\pi }}{2},\dfrac{{11\pi }}{6}} \right),\left( {\dfrac{{11\pi }}{6},2\pi } \right)
The greatest integer value of 2sinx in the intervals:
(π,7π6)\left( {\pi ,\dfrac{{7\pi }}{6}} \right) is -1
(7π6,3π2)\left( {\dfrac{{7\pi }}{6},\dfrac{{3\pi }}{2}} \right)is -2
(3π2,11π6)\left( {\dfrac{{3\pi }}{2},\dfrac{{11\pi }}{6}} \right)is -2
(11π6,2π)\left( {\dfrac{{11\pi }}{6},2\pi } \right)is -1
Therefore, we can write the given integral ∫π2π[2sin⁡x]dx\int\limits_\pi ^{2\pi } {[2\sin x]dx} as:
∫π2π[2sin⁡x]dx\int\limits_\pi ^{2\pi } {[2\sin x]dx} =∫π7π6[2sin⁡x]dx+∫7π63π2[2sin⁡x]dx+∫3π211π6[2sin⁡x]dx+∫11π62π[2sin⁡x]dx\int\limits_\pi ^{\dfrac{{7\pi }}{6}} {[2\sin x]dx + \int\limits_{\dfrac{{7\pi }}{6}}^{\dfrac{{3\pi }}{2}} {[2\sin x]dx + \int\limits_{\dfrac{{3\pi }}{2}}^{\dfrac{{11\pi }}{6}} {[2\sin x]dx + \int\limits_{\dfrac{{11\pi }}{6}}^{2\pi } {[2\sin x]dx} } } }
Substituting the values of [2sinx] in the respective integrals, we get
∫π2π[2sin⁡x]dx=∫π7π6(−1)dx+∫7π63π2(−2)dx+∫3π211π6(−2)dx+∫11π62π(−1)dx ⇒∫π2π[2sin⁡x]dx=[−x]π7π6+[−2x]7π63π2+[−2x]3π211π6+[−1x]11π62π ⇒∫π2π[2sin⁡x]dx=−[(7π6−π)+(3π2−7π6)+(11π6−3π2)+(2π−11π6)] ⇒∫π2π[2sin⁡x]dx=−[(π6+4π3+π6)]=−[π+8π+π6]=−10π6=−5π3  \int\limits_\pi ^{2\pi } {[2\sin x]dx = \int\limits_\pi ^{\dfrac{{7\pi }}{6}} {( - 1)dx + \int\limits_{\dfrac{{7\pi }}{6}}^{\dfrac{{3\pi }}{2}} {( - 2)dx + \int\limits_{\dfrac{{3\pi }}{2}}^{\dfrac{{11\pi }}{6}} {( - 2)dx + \int\limits_{\dfrac{{11\pi }}{6}}^{2\pi } {( - 1)dx} } } } } \\\ \Rightarrow \int\limits_\pi ^{2\pi } {[2\sin x]dx = } [ - x]_\pi ^{\dfrac{{7\pi }}{6}} + [ - 2x]_{\dfrac{{7\pi }}{6}}^{\dfrac{{3\pi }}{2}} + [ - 2x]_{\dfrac{{3\pi }}{2}}^{\dfrac{{11\pi }}{6}} + [ - 1x]_{\dfrac{{11\pi }}{6}}^{2\pi } \\\ \Rightarrow \int\limits_\pi ^{2\pi } {[2\sin x]dx = - \left[ {\left( {\dfrac{{7\pi }}{6} - \pi } \right) + \left( {\dfrac{{3\pi }}{2} - \dfrac{{7\pi }}{6}} \right) + \left( {\dfrac{{11\pi }}{6} - \dfrac{{3\pi }}{2}} \right) + \left( {2\pi - \dfrac{{11\pi }}{6}} \right)} \right]} \\\ \Rightarrow \int\limits_\pi ^{2\pi } {[2\sin x]dx} = - \left[ {\left( {\dfrac{\pi }{6} + \dfrac{{4\pi }}{3} + \dfrac{\pi }{6}} \right)} \right] = - \left[ {\dfrac{{\pi + 8\pi + \pi }}{6}} \right] = - \dfrac{{10\pi }}{6} = - \dfrac{{5\pi }}{3} \\\
⇒∫π2π[2sin⁡x]dx=\Rightarrow \int\limits_\pi ^{2\pi } {[2\sin x]dx} = −5π3 - \dfrac{{5\pi }}{3}
Hence, option(A) is correct.

Note: Students generally gets confused after seeing the question when G. I. F. of the function is mentioned in the integral. Take care of the graph while scaling it because we need a graph of function mentioned in the question. You are required to substitute only those values in the place of G. I. F. of the given equation which has been converted into the respective greatest integers.