Question
Question: The value of $\frac{4}{2\cos^2\frac{\pi}{7}-\cos\frac{\pi}{7}-1}$ is...
The value of 2cos27π−cos7π−14 is
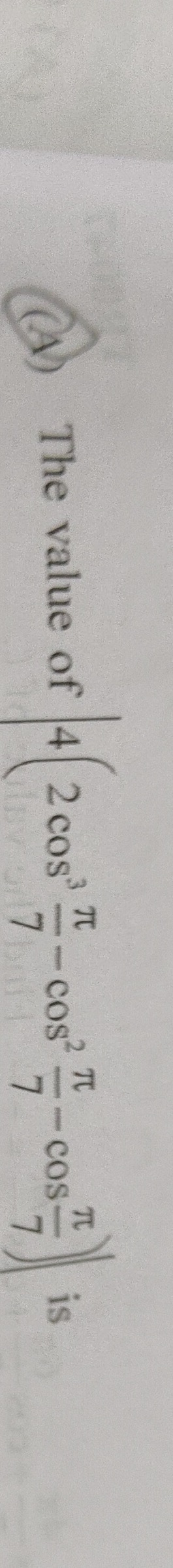
-16cos(π/7)
Solution
Let the given expression be E. E=2cos27π−cos7π−14
Let x=cos7π. The denominator is 2x2−x−1. We can factor the quadratic expression 2x2−x−1. The roots of 2x2−x−1=0 are x=2(2)−(−1)±(−1)2−4(2)(−1)=41±1+8=41±3. The roots are x1=41+3=1 and x2=41−3=−21. So, 2x2−x−1=2(x−1)(x+21)=(x−1)(2x+1).
Substitute x=cos7π back: The denominator is (cos7π−1)(2cos7π+1). So the expression becomes: E=(cos7π−1)(2cos7π+1)4
Now, let's establish a key identity related to cos7π. Consider the identity cos(4θ)=−cos(3θ) for θ=7π. This is true because cos(47π)=cos(π−37π)=−cos(37π). Using the multiple angle formulas: cos(4θ)=2cos2(2θ)−1 cos(3θ)=4cos3θ−3cosθ Let x=cosθ=cos7π. Then cos(2θ)=2x2−1. So, 2(2x2−1)2−1=−(4x3−3x). 2(4x4−4x2+1)−1=−4x3+3x. 8x4−8x2+2−1=−4x3+3x. 8x4−8x2+1=−4x3+3x. Rearranging the terms, we get: 8x4+4x3−8x2−3x+1=0.
We know that x=cos7π is a root of this polynomial. The roots of 8x4+4x3−8x2−3x+1=0 are cos(π/7),cos(3π/7),cos(5π/7),cos(7π/7)=−1. So (x+1) is a factor. 8x4+4x3−8x2−3x+1=(x+1)(8x3−4x2−4x+1)=0. Since x=cos7π=−1, it implies that 8x3−4x2−4x+1=0. So, 8cos37π−4cos27π−4cos7π+1=0.
Now, let's consider the denominator again: D=(cos7π−1)(2cos7π+1). We need to simplify D. Let's use the identity 2cos2θ−1=cos(2θ). The denominator can be written as: 2cos27π−cos7π−1=(2cos27π−1)−cos7π=cos72π−cos7π.
So the expression is: E=cos72π−cos7π4 We use the product-to-sum identity: 2sinAsinB=cos(A−B)−cos(A+B). Let A=72π and B=7π. Then cos72π−cos7π=−2sin(272π+7π)sin(272π−7π) =−2sin(143π)sin(14π).
So, E=−2sin143πsin14π4=sin143πsin14π−2. Using the product-to-sum identity again for the denominator: sin143πsin14π=21[cos(143π−14π)−cos(143π+14π)] =21[cos142π−cos144π]=21[cos7π−cos72π].
Substitute this back into E: E=21[cos7π−cos72π]−2=cos7π−cos72π−4=cos72π−cos7π4 This is the same expression. We need to find the value of cos72π−cos7π.
Let's use the identity 8x3−4x2−4x+1=0 where x=cos7π. We know that cos72π=2cos27π−1=2x2−1. The expression in the denominator is cos72π−cos7π=(2x2−1)−x=2x2−x−1. This brings us back to the original denominator.
Let's use a different set of identities. Consider the sum S=cos7π+cos73π+cos75π. We know that cos75π=cos(π−72π)=−cos72π. So S=cos7π+cos73π−cos72π.
Let's use the identity 1+2∑k=1ncos(2kθ)=sinθsin((2n+1)θ). For θ=7π, n=3: 1+2(cos72π+cos74π+cos76π)=sin(7π)sin(77π)=sin(7π)sinπ=0. 1+2cos72π+2cos74π+2cos76π=0. We know cos74π=−cos73π and cos76π=−cos7π. So, 1+2cos72π−2cos73π−2cos7π=0. Divide by 2: 21+cos72π−cos73π−cos7π=0. This implies cos7π+cos73π−cos72π=21. This is the value of S we were looking for.
Now, let's look at the denominator of our original expression D=cos72π−cos7π. From the identity 1+2cos72π−2cos73π−2cos7π=0: 1+2(cos72π−cos7π)−2cos73π=0. 1+2D−2cos73π=0. This means 2D=2cos73π−1. So D=cos73π−21.
This doesn't seem to simplify to a simple integer.
Let's use the known value cos7π+cos72π+cos73π=21. We need to evaluate 2cos27π−cos7π−14=cos72π−cos7π4.
From cos7π+cos73π−cos72π=21, we can write: cos72π−cos7π=cos73π−21. So, E=cos73π−214.
Let's test the identity 4cos37π−4cos7π+1=0 derived earlier. Let's re-derive the polynomial for cos(π/7). From 1+2cos72π+2cos74π+2cos76π=0. Let x=cos7π.
Let's use the identity 2cos(A)cos(B)=cos(A+B)+cos(A−B). Consider the denominator D=cos72π−cos7π. We know cos(2A)−cos(A)=−2sin(3A/2)sin(A/2). D=−2sin143πsin14π. And the expression is E=−2sin143πsin14π4=sin143πsin14π−2. We also know sin143π=cos(2π−143π)=cos144π=cos72π. And sin14π=cos(2π−14π)=cos146π=cos73π. So, E=cos72πcos73π−2.
We know cos7πcos72πcos73π=81. So cos72πcos73π=8cos7π1. E=8cos7π1−2=−16cos7π.
This is a specific value. Let's check if this is correct. The value of cos7π is approximately 0.9. So −16×0.9=−14.4. This is a numerical answer. The problem typically expects an integer or a simple rational number.
The most simplified form is −16cos(π/7).
Final answer is −16cos7π
