Question

The value of escape velocity on the earth is,
(A) $11.2km{{s}^{-1}}$
(B) $11.2km{{s}^{-2}}$
(C) $10.2km{{s}^{-1}}$
(D) $11.2m{{s}^{-2}}$

Answer 1

The law of energy conservation is applicable all over the world. For the earth particle system, it is also applicable. So, the velocity when the particle escapes from the earth is obtained by the total initial energy and total final energy of the earth particle system, and both energies are the same.
Formula used:
Energy conservation: ${{E}_{i}}={{E}_{f}}$
Kinetic energy: $K=\dfrac{1}{2}m{{v}^{2}}$
Gravitational potential energy: ${{E}_{m}}=\dfrac{GMm}{R}$

Complete answer:
From the law of energy conservation the total energy of the system remains the same in all situations.
Consider the mass $m$on the surface of the earth. When the mass is thrown from the surface of the earth it comes back because of the gravitational force of the earth but when sufficient velocity is given to it , it escapes the earth surface. Assume that the mass escapes with velocity $v$, given in figure.

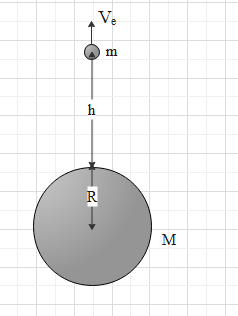
At the surface of the earth, the total initial energy is,
${{E}_{i}}=\dfrac{GMm}{R}$
At the height$h$, the total energy is,
${{E}_{f}}=\dfrac{1}{2}m{{v}_{e}}^{2}$
Using energy conservation,
${{E}_{i}}={{E}_{f}}$
$\therefore \dfrac{GMm}{R}=\dfrac{1}{2}m{{v}_{e}}^{2}$
$\therefore {{v}_{e}}^{2}=\dfrac{2GM}{R}$
But as we know $\dfrac{GM}{{{R}^{2}}}=g$ where $g$is the gravitational acceleration on the earth.
$\therefore {{v}_{e}}^{2}=2gR$
$\therefore {{v}_{e}}=\sqrt{2gR}$
Now putting the value of the $g$and $R$,
$g=9.8m{{s}^{-1}}$
$R=6400km$
$\therefore {{v}_{e}}=\sqrt{2\times 9.8\times 6400}$
$\therefore {{v}_{e}}=11.2km{{s}^{-1}}$

So, the correct answer is “Option A”.

Note:
Escape velocity is the minimum velocity needed by the body to be projected to overcome the gravitational force of the earth. The escape velocity does not depend upon the mass of the escaping body, so the small particle or very large particle can escape from the earth with the same escape velocity.