Question
Question: The value of effective resistance between \(A\) and \(B\) is? \(\left( {Given\,\,R = 2k\Omega } \rig...
The value of effective resistance between A and B is? (GivenR=2kΩ)
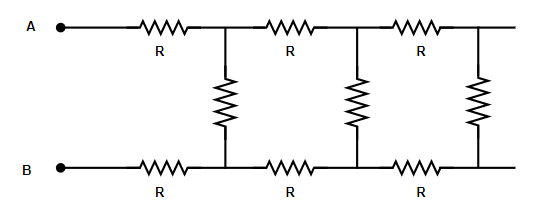
(a)(1+3)kΩ
(b)2(1+3)kΩ
(c)(1−3)kΩ
(d)2(1−3)kΩ
Solution
Whenever you are given with a question where resistances or capacitances are connected in a similar pattern up to ′n′ number of times, firstly find unit cell of the network then assume x or y as the combined resistance for the rest of pattern (n−1) number of times. This pattern is also known as the infinite ladder network.
Formula used:
(A) r=r1+r2+r3+...........+rn (when resistance are connected in series)
(B) r1=r11+r21+r31+.............+rn1 (when resistance are connected in parallel)
Complete step by step answer:
Let us assume that equivalent resistance or effective resistance for this network is Req . Here, in this problem, the unit cell of network is shown in below picture as follows:
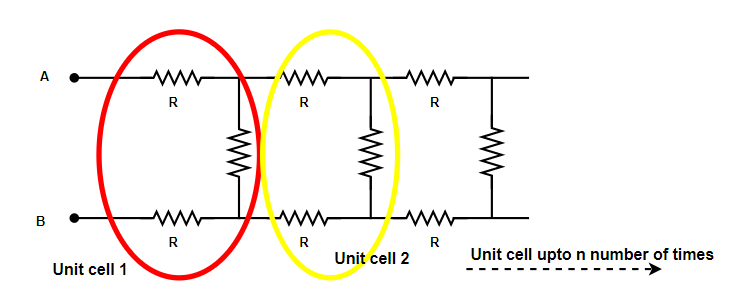
Thus, your first basic step in the question is to find a unit cell of the network in circuit.
Let the combined resistance for the rest of the network (except the resistance of unit cell 1) be x .
⇒RAB=x
Where, RAB is equal to the combined resistance of (n−1) unit cells.
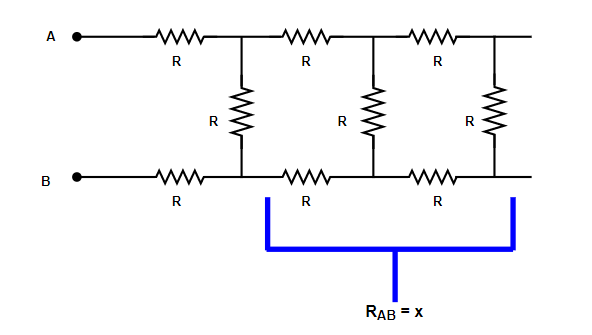
Then,
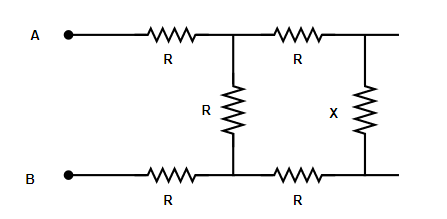
Also,
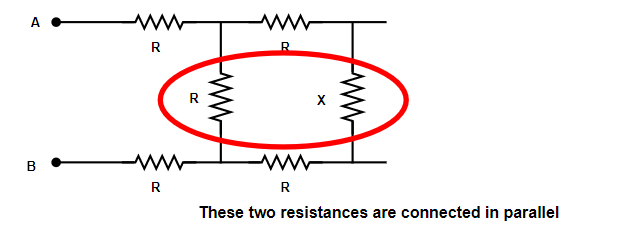
From the figure, the combined resistance r for parallel combination is given by
r1=r11+r21+r31+.............+rn1 (When resistance are connected in parallel)
And it can be written as
⇒r1=R1+x1
Now on solving it, we get
⇒r1=xRx+R
Solving it, we get
⇒r=x+RxR and we will let it eq. 1
Next, from the below shown figure, it’s clear that all the three resistances are in connected in series,
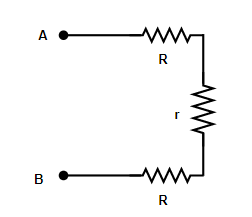
∴ By applying, r=r1+r2+r3+...........+rn (when resistance are connected in series) we get,Req=R+r+R and we will let it eq. 2
Also, given in question that, R=2KΩ and from above eq. 1 , substituting values in eq. 2 , we get as follows:
⇒Req=2+2+x2x+2
And on solving it, we get
⇒Req=4+2+x2x
Now, Req≈RAB
⇒Req=x , thus
⇒x=4+2+x2x
Now on doing the cross multiplication, we get
⇒x(2+x)=4(2+x)+2x
And on solving it, we get
⇒2x+x2=8+4x+2x
Further doing the solution,
⇒x2=8+4x
Or it can be written as
⇒x2−4x−8=0
By applying the formula for finding roots of a quadratic equation, 2a−b±b2−4ac , We get,
⇒24±16+32
On solving it,
⇒24±48
And it will be equal to
⇒2(1±3)
Now the value of 3=1.7320, so 1−3 have negative value, and resistance can’t have a negative value.
∴x=2(1+3) would be the effective resistance to give an infinite ladder network.
⇒ Option (b) is correct.
Note: Do not confuse yourself with why we putReq≈RAB , because ladder continues up to infinity, therefore, resistance of 1unit cell would be very-very small and can be negligible. Always, consider the positive value of resistance instead a negative value. Try to simplify the network step by step to reduce any error.
