Question

The value of $\dfrac{6}{\pi }\int\limits_{\dfrac{\pi }{6}}^{\dfrac{\pi }{3}}{[2\sin x]}\,dx$ , where [.] represents the greatest integer function.
(a) 1
(b) 2
(c) 3
(d) 0

Answer 1

In order to solve this problem, we need to solve the greatest integer function first. The greatest integer function rounds off to the integer less than the actual number. It is also called the step function. We need to understand the behaviour of the graph under the limits given and find the greatest integer value of that function.

Complete step by step answer:
We are given a function of $\left[ 2\sin x \right]$ and we need to integrate it under certain limits,
Let’s draw the function of $2\sin x$ and try to understand it better.

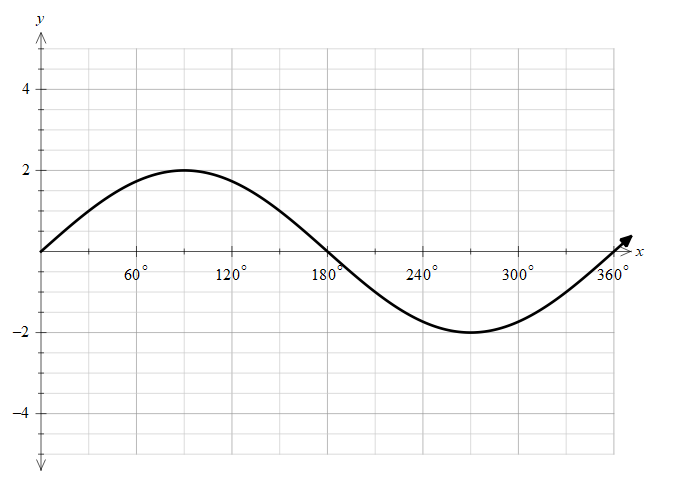
Due to the factor of two, the maximum amplitude of the function is now raised to 2.
Now let’s understand the meaning of greatest integer function.
The greatest integer function rounds off to the integer less than the actual number.
It is also called the step function.
If the value of the function is between 1 and 2 the greatest integer function we make it value 1.
Now we need to find the value of x where the function has integer values.
Let's find where $2\sin x=0$ ,
Solving for x we get,
$\begin{aligned} & 2\sin x=0 \\\ & \sin x=0 \\\ & x=0 \\\ \end{aligned}$
Now let’s find where the function becomes 1.
$\begin{aligned} & 2\sin x=1 \\\ & \sin x=\dfrac{1}{2} \\\ & x=\dfrac{\pi }{6} \\\ \end{aligned}$
Moving on let’s find where the function becomes 2.
$\begin{aligned} & 2\sin x=2 \\\ & \sin x=1 \\\ & x=\dfrac{\pi }{2} \\\ \end{aligned}$
Now we have all the integer values, we can solve the integration.
$\dfrac{6}{\pi }\int\limits_{\dfrac{\pi }{6}}^{\dfrac{\pi }{3}}{[2\sin x]}\,dx$
In the range of $\dfrac{\pi }{6}$ to, $\dfrac{\pi }{3}$ we can see from the graph that the function is increasing and it get the value of 1 at $x=\dfrac{\pi }{6}$ . Therefore, we need to round off the function to 1, as the function is between 1 and 2 through the interval.
Hence, by substituting we get,
$\dfrac{6}{\pi }\int\limits_{\dfrac{\pi }{6}}^{\dfrac{\pi }{3}}{[2\sin x]}\,dx=\dfrac{6}{\pi }\int\limits_{\dfrac{\pi }{6}}^{\dfrac{\pi }{3}}{1.}dx$
Solving this further we get,

& \dfrac{6}{\pi }\int\limits_{\dfrac{\pi }{6}}^{\dfrac{\pi }{3}}{1.}dx=\dfrac{6}{\pi }\left( \dfrac{\pi }{3}-\dfrac{\pi }{6} \right) \\\ & =\dfrac{6}{\pi }\times \dfrac{\pi }{6} \\\ & =1 \end{aligned}$$ **So, the correct answer is “Option a”.** **Note:** In this problem, we must understand that any value of the greatest integer function is going to an integer only. We always need to choose the lower limit of the function that has value between the two integers. Also, If the function crosses the integer limit then we need to split the integration into two with different limits.