Question

The value of current through $2\Omega$ resistor is

(A) $1.0A$
(B) $1.5A$
(C) $5.0A$
(D) $2.1A$

Answer 1

The currents that pass through each resistor are marked and their values found out. The entire circuit is then divided into two loops. The question can be solved by applying Kirchhoff’s Voltage Law to the loops formed.

Complete Step by Step Solution:
Kirchhoff's voltage law (KVL) states that the sum of all voltages around any closed loop in a circuit must be equal to zero. This is a consequence of charge conservation and also conservation of energy. This means that the sum of all potential differences across the component involved in the circuit gives a zero reading, as expected.
We redraw the diagram as shown below.

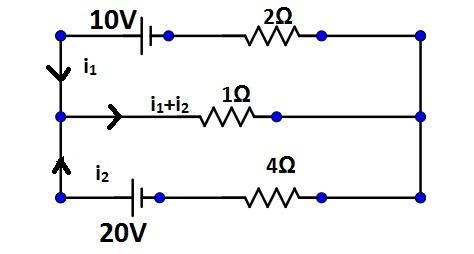
Thus,${i_1}$ is the current generated by the source of 10V and ${i_2}$ is the current generated by the 20V source.
The current passing through the resistor $1\Omega$ is the sum of ${i_1}$ and ${i_2}$ currents. Similarly, the current through the resistor $4\Omega$ is of value ${i_2}$, and the value of current passing through the $2\Omega$ resistor is of value ${i_1}$. This has been shown in the figure.
Thus there are two loops formed. Let us call the lower loop, the one with source of 20V as Loop 1 and the loop with the source 10V as Loop 2.
We apply Kirchhoff’s voltage Law to both the loops.
In the first loop of 20V, we have,
$1\left( {{i_1} + {i_2}} \right) + 4{i_2} - 20 = 0$
$\Rightarrow 5{i_2} + {i_1} = 20$.
By applying KVL in loop 2 of 10V, we get,
$\left( {{i_1} + {i_2}} \right) + 2{i_1} - 10 = 0$
$\Rightarrow 3{i_1} + {i_2} = 10$
From both the equations, we can write,
$5{i_2} + {i_1} = 20$ and
$2\left( {3{i_1} + {i_2}} \right) = 2 \times 10 = 20$.
Thus,
$5{i_2} + {i_1} = 6{i_1} + 2{i_2}$
$\Rightarrow 3{i_2} = 5{i_1}$
Again, from the equations of the loops it can be written that,
$14{i_1} = 30$
$\Rightarrow {i_1} = \dfrac{{15}}{7} = 2.1A$
The value of current through the $2\Omega$ resistor is given by the value of ${i_1}$.

Thus, the correct answer is Option D.

Note: For the second loop, where the source is of emf 20V, we have current ${i_2}$.
We know that, ${i_2} = \dfrac{5}{3}{i_1}$ and ${i_1} = \dfrac{{15}}{7}$. Thus,
${i_2} = \dfrac{5}{3} \times \dfrac{{15}}{7} = \dfrac{{25}}{7} = 3.571A$