Question

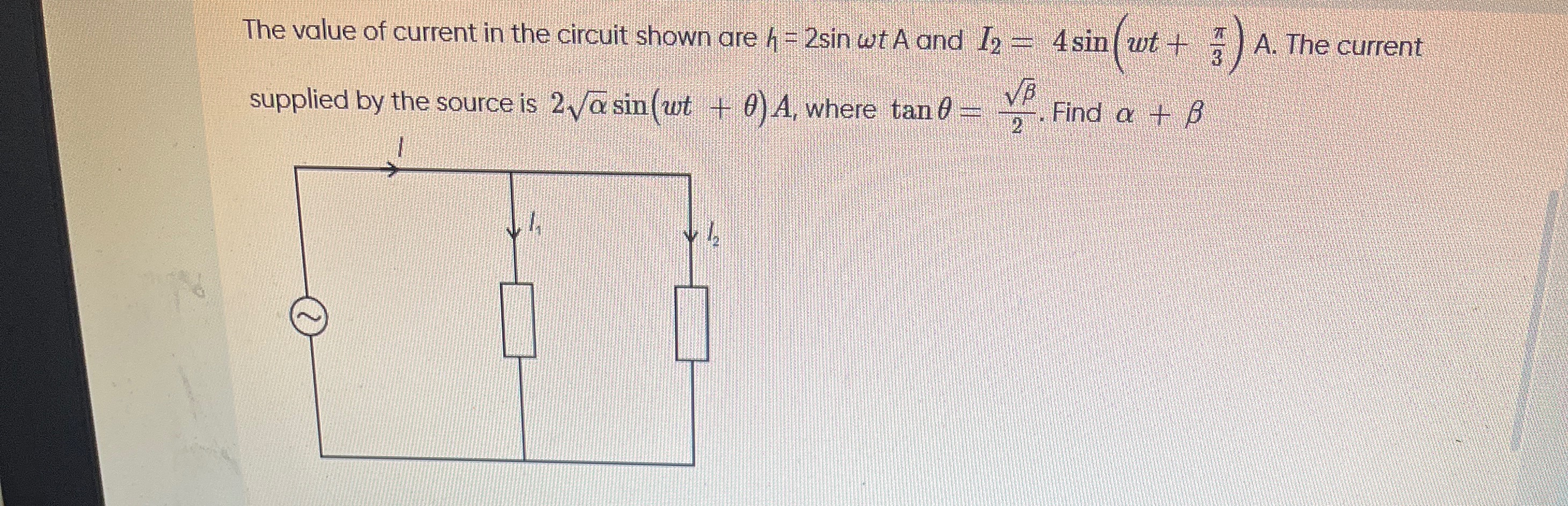
The value of current in the circuit shown are $I_1 = 2 \sin wt$ A and $I_2 = 4 \sin (wt + \frac{\pi}{3})$ A. The current supplied by the source is $2\sqrt{\alpha} \sin(wt + \theta)$ A, where $\tan \theta = \frac{\sqrt{\beta}}{2}$. Find $\alpha + \beta$

Answer 1

10

Answer 2

The problem involves finding the sum of two sinusoidal currents in parallel branches to determine the total current supplied by the source. We will use the phasor method for adding AC currents.

Given currents are:

1. $I_1 = 2 \sin wt$ A
2. $I_2 = 4 \sin (wt + \frac{\pi}{3})$ A

The total current supplied by the source is $I = I_1 + I_2$. We can represent these currents as phasors: $I_1$ has an amplitude $I_{1m} = 2$ A and a phase angle $\phi_1 = 0$ radians. In rectangular form: $I_1 = 2 \cos 0^\circ + j 2 \sin 0^\circ = 2 + j0$

$I_2$ has an amplitude $I_{2m} = 4$ A and a phase angle $\phi_2 = \frac{\pi}{3}$ radians (or $60^\circ$). In rectangular form: $I_2 = 4 \cos 60^\circ + j 4 \sin 60^\circ$ We know $\cos 60^\circ = \frac{1}{2}$ and $\sin 60^\circ = \frac{\sqrt{3}}{2}$. $I_2 = 4 \left(\frac{1}{2}\right) + j 4 \left(\frac{\sqrt{3}}{2}\right) = 2 + j 2\sqrt{3}$

Now, add the currents in rectangular form to find the total current $I$: $I = I_1 + I_2 = (2 + j0) + (2 + j 2\sqrt{3})$ $I = (2+2) + j (0 + 2\sqrt{3})$ $I = 4 + j 2\sqrt{3}$

To express the total current in the form $I_m \sin(wt + \theta)$, we need to convert $I$ from rectangular form ($X + jY$) to polar form ($I_m \angle \theta$). The amplitude $I_m$ is the magnitude of the complex number: $I_m = \sqrt{X^2 + Y^2}$ $I_m = \sqrt{4^2 + (2\sqrt{3})^2}$ $I_m = \sqrt{16 + (4 \times 3)}$ $I_m = \sqrt{16 + 12}$ $I_m = \sqrt{28}$ $I_m = \sqrt{4 \times 7} = 2\sqrt{7}$ A

The phase angle $\theta$ is given by: $\tan \theta = \frac{Y}{X}$ $\tan \theta = \frac{2\sqrt{3}}{4}$ $\tan \theta = \frac{\sqrt{3}}{2}$

So, the total current is $I = 2\sqrt{7} \sin(wt + \theta)$ A, where $\tan \theta = \frac{\sqrt{3}}{2}$.

The problem states that the current supplied by the source is $2\sqrt{\alpha} \sin(wt + \theta)$ A, where $\tan \theta = \frac{\sqrt{\beta}}{2}$.

By comparing the amplitude expressions: $2\sqrt{\alpha} = 2\sqrt{7}$ $\sqrt{\alpha} = \sqrt{7}$ $\alpha = 7$

By comparing the expressions for $\tan \theta$: $\frac{\sqrt{\beta}}{2} = \frac{\sqrt{3}}{2}$ $\sqrt{\beta} = \sqrt{3}$ $\beta = 3$

Finally, we need to find $\alpha + \beta$: $\alpha + \beta = 7 + 3 = 10$