Question

The value of $cosec\,{90^ \circ } =$?

Answer 1

Hint : Here in this question, we have to find the value of trigonometric ratio cosecant, angle of ${90^ \circ }$ or $\dfrac{\pi }{2}$. This can be found by using the right angle triangle and its property. And later by using the definition of trigonometric ratios and on further simplification, we get the required solution.

Complete step-by-step answer :

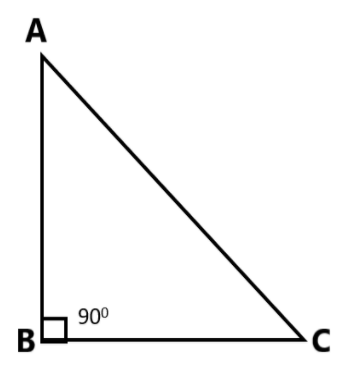
Let us calculate the trigonometric ratios cosecant of ${90^ \circ }$ which is equal to ${\dfrac{\pi }{2}^c}$ i.e., ${90^ \circ } = {\dfrac{\pi }{2}^c}$.
Consider a right angled triangle $\Delta \,ABC$ at an angle $\left| \\!{\underline {\, B \,}} \right. = {90^ \circ }$.
In $\Delta \,ABC$, when angle $\left| \\!{\underline {\, A \,}} \right.$ is very close to ${0^ \circ }$, angle $\left| \\!{\underline {\, C \,}} \right.$ is very close to ${90^ \circ }$, side AC is nearly the same as side AB.
For finding the trigonometric ratios, we need to know the lengths of the sides of the triangle. So, let us suppose that $AB = AC$ Then,
Now, use the definition of trigonometric ratios
Definition of sine ratio at $\left| \\!{\underline {\, C \,}} \right. = {90^ \circ } = \dfrac{\pi }{2}$ is:
$\sin \left( {9{0^ \circ }} \right) = \dfrac{{Opposite}}{{Hypotenuse}}$
In $\Delta \,ABC$, AB be the opposite side, BC is adjacent side with respect to the angle $\left| \\!{\underline {\, C \,}} \right.$ and AC be the hypotenuse side, then by the definition of sine ratio becomes
$\Rightarrow \,\sin \left( {9{0^ \circ }} \right) = \dfrac{{AB}}{{AC}}$
At $AB = AC$, then
$\Rightarrow \,\sin \left( {9{0^ \circ }} \right) = \dfrac{{AB}}{{AB}}$
On simplification, we get
$\Rightarrow \,\sin \left( {9{0^ \circ }} \right) = 1$
As we know, by the definition of trigonometric ratios cosecant is a reciprocal of sine.
Cosecant ratio at $\left| \\!{\underline {\, A \,}} \right. = {90^ \circ } = \dfrac{\pi }{2}$ is:
$cosec\left( {{{90}^ \circ }} \right) = \dfrac{1}{{\sin \left( {{{90}^ \circ }} \right)}}$
On substituting value of$\sin \left( {{{90}^ \circ }} \right)$, we have
$\Rightarrow \,\,cosec\left( {{{90}^ \circ }} \right) = \dfrac{1}{1}$
On simplification, we get
$\Rightarrow \,\,cosec\left( {{{90}^ \circ }} \right) = 1$
Hence, the value of $cosec\left( {{{90}^ \circ }} \right) = 1$.
So, the correct answer is “1”.

Note : When solving these type of questions, first we have to know the definition of six trigonometric ratios i.e., sine, cosine, tangent, secant, cosecant and cotangent and know the property of right angled triangle and know the formula of Pythagoras theorem i.e., $hy{p^2} = op{p^2} + ad{j^2}$.